Consideramos el conjunto subyacente \(X\) si no se especifica otro conjunto.
Ejemplo 1
La topología trivial, \(\mathcal{T}_t \), es la más débil de las topologías.
$$ \mathcal{T}_t = \{\emptyset, X\}$$
Demostración
Obviamente, esta topología está contenida en cualquier topología sobre \(X\) ya que el vacío y el total siempre son abiertos.
Ejemplo 2
La topología discreta, \(\mathcal{T}_d \), es la más fina de las topologías.
$$ \mathcal{T}_d = \mathcal{P}(X) $$
Demostración
Es obvio que cualquier topología está contenida en la discreta por ser ésta el conjunto potencia.
Ejemplo 3
Sobre \(\mathbb{R}\), la topología usual, \(\mathcal{T}_u\), es más débil que la de Sorgenfrey, \(\mathcal{T}_S\).
Demostración
La topología usual es la generada por la base de abiertos
$$ \mathcal{B}_u = \{ ]a,b[ : a,b\in \mathbb{R}, a< b\} $$
Y la de Sorgenfrey, la generada por la base de abiertos
$$ \mathcal{B}_S = \{[a, b[: a,b\in\mathbb{R}, a< b \} $$
Dado \(x\), para cualquier \(B_x = ]a,b[ \in \mathcal{B}_u\) existe \(B_x' = [x, b[ \in \mathcal{B}_S\) y \(B_x'\subseteq B_x\). Por tanto, \(\mathcal{T}_u \subseteq \mathcal{T}_S\).
En cambio, \(\mathcal{T}_S \not\subseteq \mathcal{T}_u\) puesto que, por ejemplo, \([0, +\infty)\) es abierto en la de Sorgenfrey pero no en la usual.
Ejemplo 4
Sobre \(\mathbb{R}^2\), definimos las bases de abiertos siguientes:
$$ B = \{(x,y) : x^2+y^2 < r^2, r\in\mathbb{R}\} $$
$$ B' = ]x-\varepsilon ,x+\varepsilon[ \times ]y-\varepsilon ,y+\varepsilon[: x,y\in\mathbb{R}, \varepsilon \geq 0 $$
Ambas bases generan topologías equivalentes.
Demostración
Los abiertos de la primera base son bolas abiertas de radio \(r\). Los de \(\mathcal{B}'\) son cuadrados abiertos de lado \(2\varepsilon\).
Es fácil ver que las topologías son equivalentes:
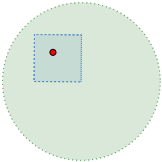
Dado un punto \((x,y)\) de una bola, existe un cuadrado abierto de la base \(\mathcal{B}'\) contenida en la bola y que contiene a dicho punto. También, podemos encontrar bolas abiertas contenidas en los cuadrados abiertos.
Ejemplo 5
Las topologías sobre \(\mathbb{R}^n\) que inducen las métricas euclídea, del máximo y de Taxicab (definidas en espacios métricos) son equivalentes.
Ejemplo 6
Sobre \(\mathbb{R}\), se define la topología cofinita como
$$ \mathcal{T}_{cof} = \{A\subseteq \mathbb{R}: A-\mathbb{R}\text{ es finito ó } A = \emptyset\} $$
Sea \(\mathcal{T}'\) la topología definida por la base
$$ \mathcal{B}' = \{A : \mathbb{R}-A \text{ es un subconjunto acotado de }\mathbb{Z}\}$$
La topología cofinita es más fina que \(\mathcal{T} '\).
Demostración
Para todo \(B \in \mathcal{B}'\), \(\mathbb{R}-B\) es un subconjunto acotado de \(\mathbb{Z}\), así que es finito o vacío y, por tanto, \(B\) es abierto en la topología cofinita. Luego \( \mathcal{T}' \subseteq \mathcal{T}_{cof}\).
El conjunto \(A = \mathbb{R}-\{\pi\}\) es un abierto en la cofinita, pero no lo es en \(\mathcal{T}'\) porque dado \(x\) de \(A\), no existe \(B\in\mathcal{B}'\) tal que \(x\in B \subseteq A\).


Compación de topologías (con ejemplos) - © matesfacil.com

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.




