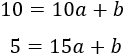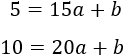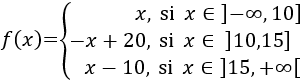Primera parte: 4 problemas sobre funciones definidas por partes.
Problema 1
Dada la siguiente función definida a trozos
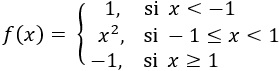
Se pide:
-
Calcular la imagen de los puntos \(x = -3\), \(x = -1\), \(x = 0\), \(x = 1\) y \(x = 5\).
-
Expresar la misma función con intervalos, es decir, utilizando intervalos en lugar de los signos de desigualdad.
-
Representar la gráfica (con puntos sólidos o vacíos en los extremos de los intervalos).
-
Observando la gráfica, ¿\(f\) es una función continua?
Ver solución
Apartado a:
Como \(x=-3\) es menor que -1, debemos utilizar la primera definición:
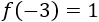
Como \(x = -1\) es mayor o igual que -1 y menor que 1, debemos utilizar la segunda definición. También para \(x = 0\):
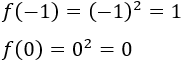
Como \(x=1\) y \(x = 5\) son mayores o iguales que 1, debemos utilizar la tercera definición:
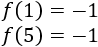
Apartado b:
Escribimos la función con intervalos:
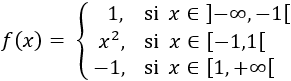
O bien, si utilizamos paréntesis para los intervalos abiertos,
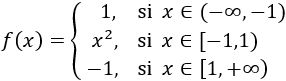
Apartado c:
Como la función tiene tres definiciones, tenemos que dibujar tres trozos de funciones.
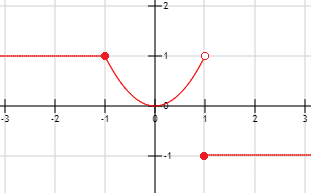
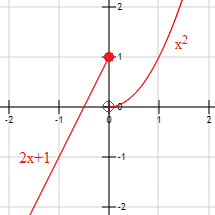
Para \(x < -1\), la gráfica es la recta constante \(y = 1\); para \( -1\leq x < 1\), la gráfica es la parábola \(y = x^2\); y para \(x \geq 1\), la gráfica es la recta constante \(y = -1\). Los puntos deben ser sólidos en los extremos cerrados de los intervalos.
La gráfica es
Apartado d:
La función no es continua puesto que en el extremo \(x = 1\) hay un salto. Sin embargo, en el extremo \(x = -1\) la función es continua.
La función es continua en \(\mathbb{R}-\{1\}\).
Problema 2
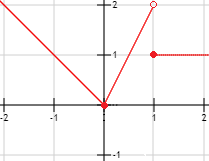
Determinar la función por partes cuya gráfica es la siguiente:
Calcular los siguientes límites:
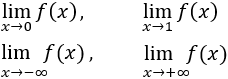
Ver solución
Observando la gráfica, ya sabemos que la función tiene tres definiciones. Los intervalos para las definiciones son:
![]-infinito, 0], ]0,1[ y [1, +infinito[ Funciones definidas a trozos. Conceptos básicos, continuidad, límites laterales. Problemas resueltos de aplicación y de los conceptos. Problemas para Bachillerato. Análisis de una variable real](https://www.matesfacil.com/BAC/funciones/trozos/P2-1.png)
En el primer intervalo hemos incluido el punto 0 y lo hemos excluido en la segundo. Pero podíamos haber escogido lo contrario ya que la función tiende al mismo punto en ambos intervalos y \(f(0) = 0\):
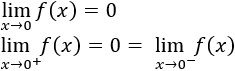
En el segundo intervalo hemos excluido el punto 1 ya que la imagen de la función es \(f(1) = 1\) y no \(f(1) = 2\). El límite en \( x = 1\) no existe porque los límites laterales no coinciden:
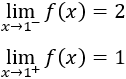
En el primer intervalo, la definición de la función es \(f(x) = -x\); en el segundo, \(f(x) = 2x\); y en el tercero, \(f(x) = 1\). Por tanto, la función es
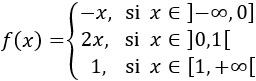
Si utilizamos paréntesis para los intervalos abiertos,
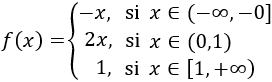
Finalmente, los límites en los infinitos son
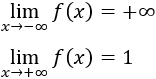
Problema 3
Dada la función definida a trozos
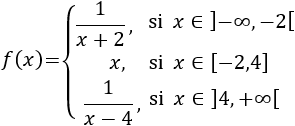
Se pide, sin representar la gráfica:
-
Calcular los límites laterales de \(f\) en los extremos de los intervalos de definición de la función.
-
Calcular el límite de \(f\) en los puntos \(x = -2\) y \(x = 4\).
-
Determinar los puntos de discontinuidad de la función.
Representar la gráfica según los resultados anteriores.
Ver solución
Apartado a:
Los límites en los extremos del primer intervalo son
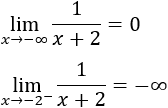
Los límites en los extremos del segundo intervalo son
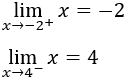
Los límites en los extremos del tercer intervalo son
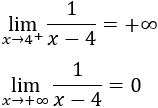
Apartado b:
El límite de \(f\) no existe en \(x = -2\) ni en \(x = 4\) ya que los límites laterales no coinciden:
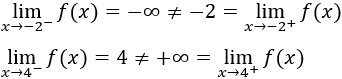
Apartado c:
Los puntos donde la función es discontinua son \( x = -2\) y \(x = 4\). En los otros puntos la función es continua.
Apartado d:
La gráfica de la función es
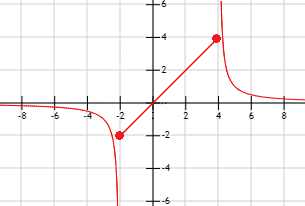
Tiene una asíntota horizontal en \(y = 0\) y asíntotas verticales en \(x = -2\) y en \(x =4\) por la izquierda y por la derecha, respectivamente.
Problema 4
Representar la siguiente función a trozos:
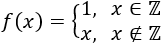
Responder:
-
¿Es una función continua?
-
¿Cuál es el límite de \(f(x)\) cuando \(x\) tiende a un número entero?
-
¿Cuáles son los puntos de discontinuidad de \(f\)?
Ver solución
La gráfica de la función es
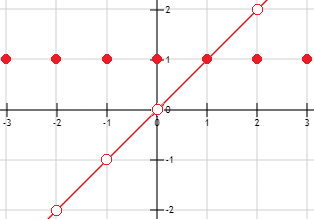
Apartado a:
No es una función continua porque, por ejemplo, el límite de \(f(x)\) cuando \(x\) tienda a -1 es -1, mientras que la imagen de -1 es 1 (hay un salto).
Apartado b:
El límite de \(f(x)\) cuando \(x\) tiende a un entero es dicho entero:
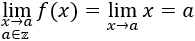
Apartado c:
Los puntos de discontinuidad son todos los enteros excepto 1 ya que en \(x=1\) el límite de \(f(x)\) coincide con \(f(1)\).
Segunda parte: 6 problemas de aplicación.
Problema 5
Una sala de fiestas de la Ciudad de México con aforo para 300 personas establece el precio de la entrada cada día en función del número de asistentes que se prevé que habrá en dicho día:
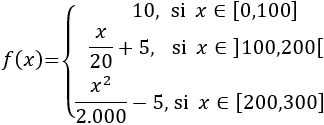
Se pide:
-
¿Cuál es el precio de una entrada si se espera que asistan 50 personas? ¿Y si son 110? ¿Y si son 200? ¿Y si se espera que se agoten las entradas?
-
¿Cuáles son los ingresos totales si se espera que asistan 150 personas? ¿Y si sólo son 90?
-
¿Cuántas personas deberían asistir para que el precio de la entrada supere los $30?
-
Representar la función.
-
¿Cuál es el precio máximo y mínimo de una entrada?
Ver solución
Apartado a:
Si asisten 50 personas, estamos en el primer intervalo. Por tanto, el precio de una entrada es $10.
Si asisten 110 personas, estamos en el segundo intervalo. Por tanto, el precio es $10.5:
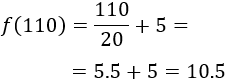
Si asisten 200 personas, estamos en el tercer intervalo. Por tanto, el precio es $15:
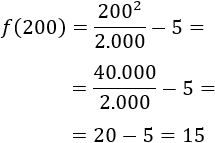
Si asisten 300 personas, estamos en el tercer intervalo. Por tanto, el precio es $40:
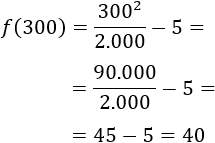
Apartado b:
Si asisten 150 personas, estamos en el segundo intervalo. Por tanto, el precio por entrada es $12.5:
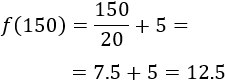
Luego los ingresos totales son $1.875:
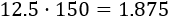
Si asisten 90 personas, estamos en el primer intervalo. Por tanto, el precio por entrada es $10 y los ingresos suman $900.
Apartado c:
Si el precio de una entrada asciende a $30 es porque se esperan más de 100 personas (el primer intervalo queda descarado).
Tenemos que resolver la ecuación
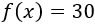
Si suponemos que la cantidad de asistentes es menor que 200, tenemos la ecuación
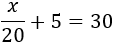
cuya solución es 500, pero este resultado no es menor que 200, así que suponemos que la solución debe estar en el tercer intervalo.
Tenemos la ecuación
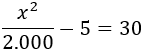
La resolvemos:
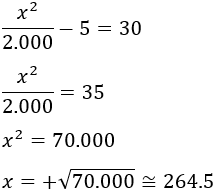
Como la función \(x^2/2.000-5\) es creciente (para \(x \geq 1\)), el precio de la entrada supera los $30 cuando se espera que asistan al menos 265 personas.
Apartado d:
La gráfica de la función es
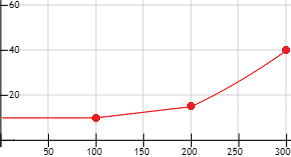
Apartado e:
El precio mínimo de una entrada es $10. El precio máximo se $40, que se alcanza cuando se espera llenar el aforo (lo hemos calculado anteriormente):
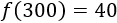
Problema 6
El equipo de merchandising de un equipo de fútbol español fabrica diariamente banderines para suplir los pedidos de las tiendas. La gráfica de la función que proporciona la cantidad diaria de banderines a fabricar en función del número de pedidos es la siguiente:
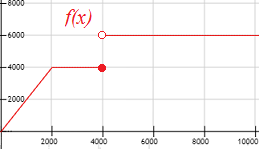
Nota: se considera que el número de pedidos, \(x\), es una variable real (puede tener decimales).
Se pide:
-
¿Cuántos banderines se fabrican si la cantidad de pedidos es 2.500? ¿Y si es 4.000? ¿Y si es mayor que 5.000? ¿Y si es 1.000?
-
¿Cuántos pedidos deben recibirse para que se fabriquen 4.000 banderines? ¿Y 6.000? ¿Y 2.500?
-
¿Cuál es el número máximo de banderines que pueden fabricarse en un día?
-
¿A partir de cuántos pedidos se alcanza la cantidad máxima de fabricación?
-
Determinar la definición de la función a trozos de la función \(f\).
Ver solución
Apartado a:
El número de banderines que se fabrican si se reciben 2.500 y 4.000 pedidos es 4.000:
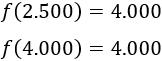
Si la cantidad de pedidos es mayor que 5.000, se fabrican 6.000 banderines.
Observando la gráfica, puede deducirse que se fabrican 2.000 banderines si el número de pedidos es 1.000. No obstante, vamos a calcular la expresión analítica de la función cuando \(0\leq x\leq 2.000\) para ser más meticulosos.
La gráfica es una función lineal (una recta) que une los puntos (0,0) y (2.000, 4.000). La función de una recta es de la forma
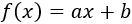
Sustituyendo el punto (0,0) obtenemos \(b\):
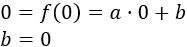
Sustituyendo el punto (2.000, 4.000) obtenemos \(a\):
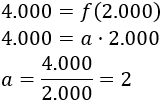
Por tanto, si \(0\leq x \leq 2.000\), la función es
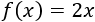
Finalmente, calculamos el número de banderines que se fabrican si se reciben 1.0000 pedidos:
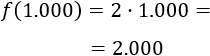
Apartado b:
Se fabrican 4.000 banderines si se reciben entre 2.000 y 4.000 pedidos (\(2.000\leq x \leq 4.000\)).
Se fabrican 6.000 banderines cuando el número de pedidos es mayor que 4.000 (\(x> 4.000\)).
Para calcular el número de pedidos necesario para que se fabriquen 2.500 banderines, utilizamos la expresión de \(f\) calculada en el apartado anterior:
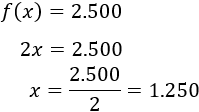
Apartado c:
El número máximo de banderines que pueden fabricarse en un día es 6.000 ya que la función \(f\) no toma valores mayores a 6.000.
Apartado d:
La función alcanza el valor 6.000 cuando la cantidad de pedidos es superior a 4.000 (es decir, \(x> 4.000\)).
Apartado e:
La definición de la función es
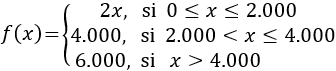
O bien, utilizando intervalos
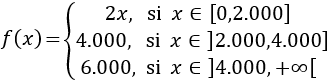
Problema 7
Antonio ha escrito un libro sobre la historia del fútbol y quiere imprimirlo para regalarlo a sus familiares y a sus amigos en su cumpleaños. Una empresa editorial le ha dado un presupuesto que dice lo siguiente:
El coste inicial para iniciar la impresión del libro es de 15€ y el precio de impresión de cada libro asciende a 5€ si se imprimen hasta 30 unidades y a 3€ si se imprimen más.
Se pide:
-
Calcular la función del coste total en función del número de libros impresos, \(f(x)\).
-
Representar la gráfica de la función \(f(x)\).
-
Si Antonio invierte 180€, ¿cuántos libros se imprimen?
-
En dicha empresa, ¿es más barato imprimir 25 libros o imprimir 40? Razonar la respuesta y relacionarla con la gráfica de \(f\).
Ver solución
Apartado a:
Si Antonio decide no imprimir ningún libro (\(x = 0\)), entonces no debe realizar ninguna inversión, así que
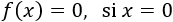
Si la cantidad de libros a imprimir es menor o igual que 30, \(0< x\leq 30\), el coste de cada libro es de 5€ y, por tanto, el coste total es
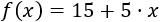
Sin embargo, si el número de libros es mayor que 30 (\(x > 30\)), el precio por cada libro es de 3€, así que el coste total es
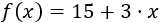
La función a trozos es
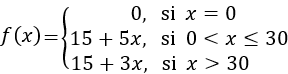
Apartado b:
La gráfica de la función es
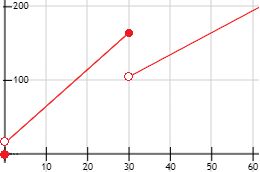
Apartado c:
Como Antonio dispone de 180€, queremos calcular la cantidad de libros \(x\) tal que \(f(x) = 180\):
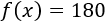
Tenemos dos ecuaciones según si \(x\) es menor o igual o mayor que 30. En el primer caso, la ecuación es
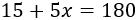
cuya solución es \(x = 33\). Pero esta solución no es buena ya que la definición utilizada es para el caso de que \(x \leq 30\).
En el segundo caso, la ecuación es
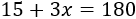
cuya solución es \( x = 55\geq 30\). Por tanto, Antonio puede imprimir 55 libros.
Apartado d:
Si se imprimen 25 libros, el coste total es 140€:
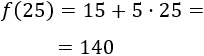
Mientras que si se imprimen 40 libros el coste total es 135€:
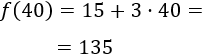
Por tanto, es más barato imprimir 40 libros que imprimir 25.
Observando la gráfica, la función \(f\) toma valores mayores que \(f(30)\) a partir de \(x = 55\). Por tanto, es más barato imprimir 31 libros que imprimir 25 ó 30.
Problema 8
El precio de una llamada a una línea telefónica de tarot se descompone en dos conceptos: el primero es el establecimiento de llamada (precio fijo) y el otro es el coste de la duración de la llamada (en función de los minutos).
El coste del establecimiento de llamada es de 0.2€ y el coste de un minuto de llamada es de 0.05€/minuto durante los primeros 60 minutos y de 0.5€/minuto a partir del minuto 60.
Se pide:
-
Calcular la función del coste total de una llamada en función de la duración de la llamada, \(f(x)\).
-
Representar la función \(f(x)\).
-
Calcular el precio de una llamada de 20 minutos y el de una llamada de 75 minutos.
-
Calcular el precio medio de un minuto de una llamada de 20 minutos y el de una de 75.
Ver solución
Apartado a:
Si la llamada dura \(x\) minutos, siendo \( 0< x\leq 60\), el coste de la llamada es el precio fijo más 0.05€/minuto. Luego la función es
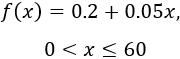
Si la llamada dura \(x\) minutos siendo \(x > 60\), el coste de la llamada es el establecimiento más \(60\cdot 0.05\) (coste los primeros 60 minutos) más \((x-60)\cdot 0.5\) (coste de los minutos restantes). Por tanto,
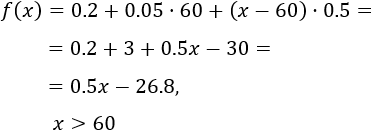
Apartado b:
La gráfica de \(f\) es
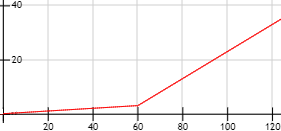
Apartado c:
El precio de una llamada de 20 minutos es 1.2€ y el de una llamada de 75 minutos es 10.7€:
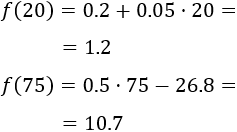
Apartado d:
Para calcular el precio medio por minuto tenemos que dividir el precio total de la llamada entre el número de minutos.
Si la duración es de 20 minutos, el precio medio es 0.06€/min:
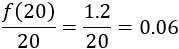
Y si es de 75 minutos, el precio medio es aproximadamente 0.14€/min:
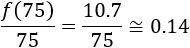
Problema 9
Un bróker (agente financiero) está estudiando la siguiente gráfica que proporciona los valores en bolsa de las acciones de la empresa de uno de sus clientes durante las 24 horas de un determinado día:
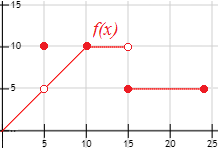
Se pide:
-
Determinar la función que describe la gráfica de \(f\).
-
¿Se trata de una función continua?
-
Calcular el límite de \(f\) en los puntos \(x =5\), \(x = 10\) y \(x = 15\).
-
En caso de haberlos, determinar los puntos de discontinuidad de \(f\). Razonar.
-
¿En qué momentos del día (\(x\)) se ha alcanzado el valor máximo?
-
¿El comportamiento del valor de las acciones es lineal? ¿Por qué?
Ver solución
Apartado a:
La función es
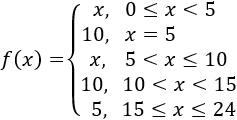
Apartado b:
No es una función continua porque tiene saltos en los puntos \(x = 5\) y \(x = 15\).
Apartado c:
Podemos calcular directamente el límite cuando \(x\) tienda a 5 porque no cambia la definición de \(f\) por sus lados:
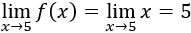
Para calcular los límites en 10 y en 15 sí que debemos calcular los límites laterales.
Límite por la izquierda de 10:
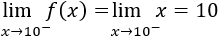
Límite por la derecha de 10:
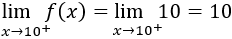
Como los límites laterales coinciden, existe el límite en \(x=10\):
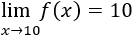
Límite por la izquierda de 15:
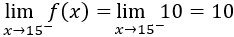
Límite por la derecha de 15:
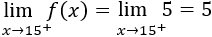
Como los límites laterales no coinciden, no existe el límite en \(x = 15\).
Apartado d:
Los únicos puntos de discontinuidad son \(x = 5\) y \(x = 15\).
En \(x = 5\) la función es discontinua porque existe el límite pero no coincide con el valor de la función (discontinuidad evitable).
En \(x = 15\) la función es discontinua porque existen los límites laterales (son finitos) pero no coinciden (discontinuidad no evitable de primera especie de salto finito).
Apartado e:
El valor máximo de la función es 10 y se alcanza en \(x = 5\) y en el intervalo [10,15).
Apartado f:
El comportamiento de la función es lineal excepto en los puntos de discontinuidad. Es creciente en las 10 primeras horas (\(x\neq 5\)) y constante en las 14 siguientes (\(x\neq 15\)).
Problema 10
Proporcionar un ejemplo de función por partes que sea continua en \(\mathbb{R}\) y lineal a trozos (lineal en los intervalos de definición) de modo que \(f(10) = 10\), \(f(15) = 5\) y \(f(20) = 10\).
Ver solución
Para que la función sea continua, tenemos que evitar que la función tenga saltos (discontinuidades). Vamos a definir \(f\) como una función lineal distinta en cada uno de los siguientes tres intervalos:
![]-infinito, 10], ]10,15] y ]15, +infinito[ Funciones definidas a trozos. Conceptos básicos, continuidad, límites laterales. Problemas resueltos de aplicación y de los conceptos. Problemas para Bachillerato. Análisis de una variable real](https://www.matesfacil.com/BAC/funciones/trozos/P10-1.png)
En el primer intervalo, como debe cumplirse que \(f(10)=10\), definimos \(f(x) = x\).
En el segundo intervalo, debe cumplirse que \(f(15)=5\). Para evitar una discontinuidad, definimos \(f\) como el segmento que une los puntos (10,10) y (15,5) sustituyendo dichos puntos en la ecuación \(y = ax+b\):
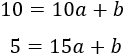
La solución del sistema es \(a = -1\) y \(b = 20\). Luego \(f(x) = -x+20\).
Para el tercer intervalo, repetimos el proceso anterior con los puntos (15,5) y (20,10):
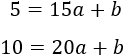
La solución del sistema es \(a = 1\) y \(b = -10\). Luego \(f(x) = x-10\).
Por tanto, la función \(f\) es
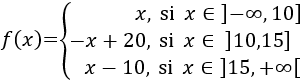
Y su gráfica es
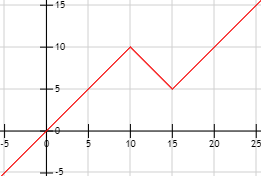

Funciones definidas a trozos - © matesfacil.com

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.

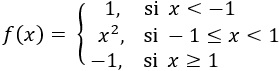
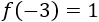
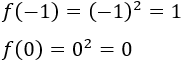
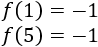
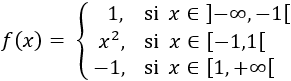
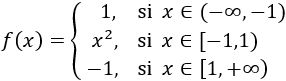


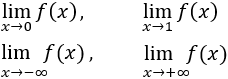
![]-infinito, 0], ]0,1[ y [1, +infinito[ Funciones definidas a trozos. Conceptos básicos, continuidad, límites laterales. Problemas resueltos de aplicación y de los conceptos. Problemas para Bachillerato. Análisis de una variable real](https://www.matesfacil.com/BAC/funciones/trozos/P2-1.png)
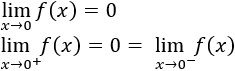
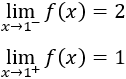
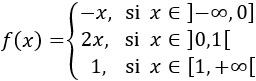
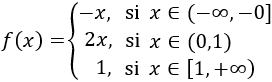
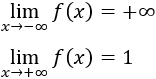
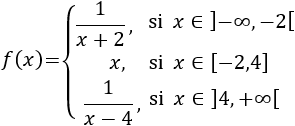
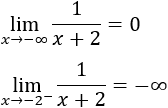
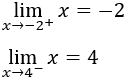
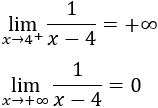
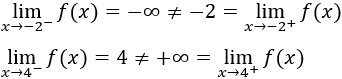

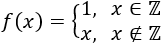

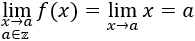
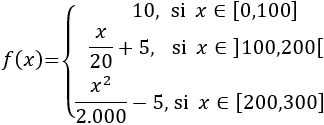
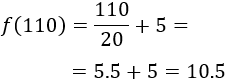
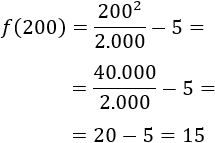
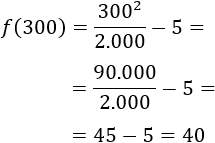
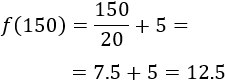
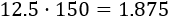
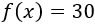
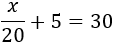
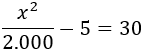
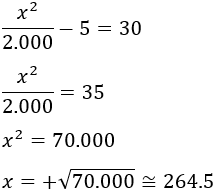

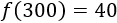

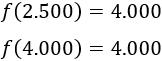
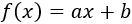
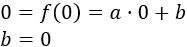
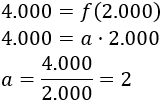
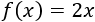
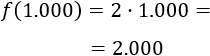
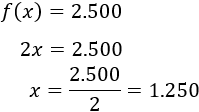
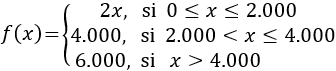
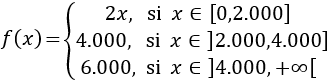
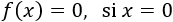
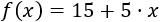
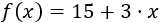
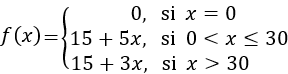

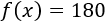
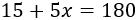
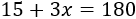
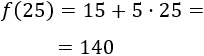
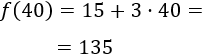
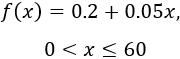
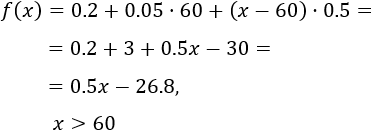

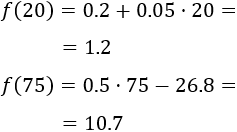
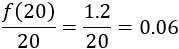
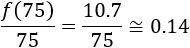

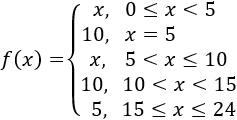
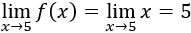
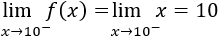
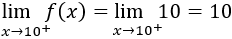
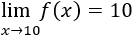
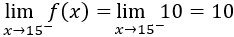
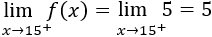
![]-infinito, 10], ]10,15] y ]15, +infinito[ Funciones definidas a trozos. Conceptos básicos, continuidad, límites laterales. Problemas resueltos de aplicación y de los conceptos. Problemas para Bachillerato. Análisis de una variable real](https://www.matesfacil.com/BAC/funciones/trozos/P10-1.png)