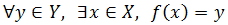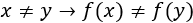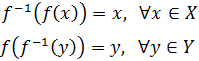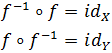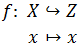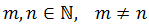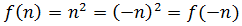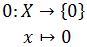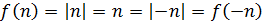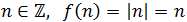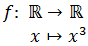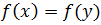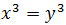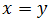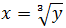Contenido de esta página:

1. Conceptos previos (dominio, codominio, imagen, etc)
2. Función sobreyectiva
3. Función inyectiva
4. Función biyectiva y función inversa

Nivel recomendado: bachillerato o superior.

Concepto de función:

Una función \(f\) del conjunto \(X\) en el conjunto \(Y\) es una ley o regla que a cada elemento \(x\) de \(X\) le hace corresponder un único elemento \(y\) de \(Y\).

 

Dominio y codominio:

A los conjuntos \(X\) e \(Y\) los llamamos dominio y codominio, respectivamente, de \(f\).

Imagen y anti-imagen:

Sea \(x\) un elemento de \(X\), llamamos imagen de \(x\) mediante \(f\) al elemento \(y\) de \(Y\) que \(f\) le hace corresponder a \(x\). En este caso, escribimos \(y=f(x)\).

El conjunto de imágenes de \(f\) se denomina imagen, rango o recorrido de la función y es un subconjunto del codominio:

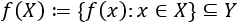
Sea \(y\) un elemento de \(Y\), su anti-imagen, si existe, es el elemento o elementos \(x\) de \(X\) tal que \(f(x)=y\).

Nota: la anti-imagen de un elemento puede ser un conjunto de elementos (más de uno). Si la función es inyectiva, la anti-imagen es un único elemento.

Ejemplo:

La función cuadrado, \(f:\mathbb{R}\rightarrow \mathbb{R}\) definida por \(f(x)=x^2\), a cada número real le hace corresponder su cuadrado.

Por ejemplo, la imagen de 1 y de -1 son

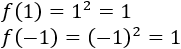
La anti-imagen de 1 es el conjunto \(\{1,-1\}\).

El dominio de \(f\) es \(\mathbb{R}\) y su codominio es \(\mathbb{R}\). La imagen de \(f\) es el conjunto de los reales no negativos:

La función \(f: X\rightarrow Y\) es sobreyectiva o suprayectiva si todo elemento del codominio tiene anti-imagen. Es decir,

Ejemplos:

• La función identidad \(f:\mathbb{R}\rightarrow \mathbb{R}\) definida por \(f(x)=x\) es sobreyectiva.
• La función valor absoluto \(f:\mathbb{R}\rightarrow \mathbb{R}\) definida por \(f(x)=|x|\) no es sobreyectiva. Por ejemplo, el punto \(-1 \in \mathbb{R}\) no tiene anti-imagen.

La sobreyectividad puede conseguirse restringiendo el codominio. Por ejemplo, la función valor absoluto definida de los reales en los reales no negativos \(f:\mathbb{R}\rightarrow \mathbb{R}^+\) es sobreyectiva.

La función \(f: X\rightarrow Y\) es inyectiva si los elementos del dominio que son distintos tienen imágenes distintas. Es decir,

Para comprobar la inyectividad de una función \(f\), se demuestra que \(f(x)=f(y)\) implica \(x=y\).

Ejemplos:

• La función nula (\(f:\mathbb{R}\rightarrow \mathbb{R},\ f(x)=0\)) no es inyectiva.
• La función cuadrado (\(f:\mathbb{R}\rightarrow \mathbb{R}, f(x)=x^2\)) no es inyectiva.
• La función identidad (\(f:\mathbb{R}\rightarrow \mathbb{R},\ f(x)=x\)) es inyectiva.
• La función mitad (\(f:\mathbb{R}\rightarrow \mathbb{R},\ f(x) = x/2\)) es inyectiva.
• La función valor absoluto (\(f:\mathbb{R}\rightarrow \mathbb{R},\ f(x)=|x|\)) no es inyectiva.

La inyectividad de una función puede conseguirse restringiendo su dominio. Por ejemplo, la función valor absoluto definida sobre los reales positivos (\(f:\mathbb{R}^+\rightarrow \mathbb{R},\ f(x)=|x|\)) es inyectiva.

La función \(f: X\rightarrow Y\) es biyectiva si es inyectiva y sobreyectiva.

En este caso, existe una función \(f^{-1}: Y\rightarrow X\) también biyectiva que cumple

Dicho de otro modo,

donde \(id_X\) e \(id_Y\) son las funciones identidad de \(X\) y de \(Y\), respectivamente. Es decir, son las funciones \(id_X: X\rightarrow X\) definida por \(id_X (x) = x\) e \(id_Y: Y\rightarrow Y\) definida por \(id_Y (y) = y\).

Ejemplo:

La función \(f:\mathbb{R}\rightarrow \mathbb{R}\) definida por \(f(x)=2x\) es biyectiva y su inversa es \(f^{-1}:\mathbb{R}\rightarrow \mathbb{R}\) definida por \(f^{-1} (y)=y/2\).

Problema 1

Comprobar que las siguientes funciones son inyectivas pero no son sobreyectivas:

1. Función mitad de los enteros en los reales:

   

2. Función cuadrado de los naturales en los reales:

   

3. Función inclusión del subconjunto propio \(X\subset Z\) en \(Z\):

   

   Nota: \(X\) es un subconjunto propio de \(Z\) si es un subconjunto de \(Z\) pero \(X\neq Z\).

Problema 2

Comprobar que las siguientes funciones son sobreyectivas pero no son inyectivas.

1. Función valor absoluto de los enteros en los naturales:

   

2. Función cuadrado de los reales en los reales no negativos:

   

   Nota: incluimos al 0 en el conjunto de los reales positivos.

3. Función nula de un conjunto \(X \subseteq \mathbb{R}\) en el conjunto \(\{0\}\):

   

Problema 3

Comprobar que las siguientes funciones son biyectivas:

1. Función identidad de \(X\):

   

2. Función cubo de los reales en los reales.

   

Problema 4

Encontrar la función inversa de cada función del Problema 3.

---