En algunos problemas se pide calcular las asíntotas y en otros, demostrar la existencia de asíntotas.
Los primeros problemas están dedicados a las asíntotas verticales; los siguientes, a las horizontales; y los últimos, a las oblicuas.
Algunas de las demostraciones pueden ser comprensibles para los alumnos de bachillerato, otras son más técnicas.
Problema 1
Encontrar las asíntotas verticales de la función racional
$$ f(x) = \frac{3}{x-1}$$
Solución
Las funciones racionales tienen asíntotas en los puntos que anulan al denominador.
El denominador de \(f\) se anula cuando \(x = 1\). Por tanto, \(x = 1\) es una posible asíntota vertical.
Calculamos el límite cuando \(x\) tiene a 1 por la izquierda:
$$ \lim_{x \to 1^- } \frac{3}{x-1} = - \infty $$
Y por la derecha:
$$ \lim_{x \to 1^+ } \frac{3}{x-1} = + \infty $$
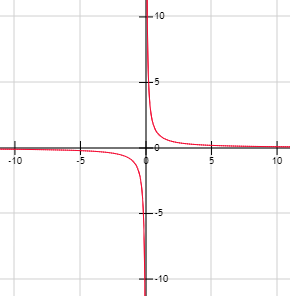
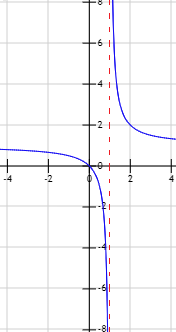
Por tanto, la recta \(x = 1\) es una asíntota vertical (por derecha e izquierda).
La gráfica de \(f\) es
Problema 2
Comprobar que una función racional
$$ f(x) = \frac{P(x)}{Q(x)} $$
donde \(P(x)\) y \(Q(x)\) son polinomios, tiene asíntotas verticales en las raíces de \(Q(x)\) que no son raíces de \(P(x)\).
Nota: demostración de dificultad baja.
Solución
Hay que demostrar que en los puntos que anulan al denominador hay asíntotas verticales.
Tenemos que comprobar el límite
$$ \lim_{x \to a} \frac{P(x)}{Q(x)} = \pm \infty $$
siendo \(a\) una raíz de \(Q\).
Sea \(a\) una raíz del polinomio del denominador que no es raíz del numerador, es decir,
$$ Q(a) = 0,\ P(a)\neq 0$$
Entonces, cuando calculamos el límite de \(P(x)/Q(x)\) cuando \(x\to a\), tendremos \(P(a)\) dividido 0. Luego el límite es infinito:
$$ \lim_{x \to a} \frac{P(x)}{Q(x)} = \pm \infty $$
Nota: si \(P\) y \(Q\) tienen la raíz común \(a\), entonces el cociente puede simplificarse y obtenerse una nueva expresión para \(f\) donde \(a\) podría dejar de ser una raíz de \(Q\).
Problema 3
¿Cuántas asíntotas verticales tiene la siguiente función?
$$ f(x) = \frac{x^2-1}{x^2+x} $$
Solución
Podríamos pensar que la función tiene dos asíntotas verticales puesto que su denominador se anula en los puntos \(x=0\) y \(x = -1\). Es por ello que lo primero que debemos hacer siempre es escribir la función en su forma más simplificada.
Factorizamos el polinomio del numerador:
$$ x^2 -1 = (x-1)(x+1)$$
Factorizamos el polinomio del denominador:
$$ x^2+x = x(x+1) $$
Luego la función puede escribirse como
$$ f(x) = \frac{(x-1)(x+1)}{x(x+1)} =$$
$$=\frac{x-1}{x} $$
La función no se puede simplificar más y, por tanto, los polinomios no tienen raíces comunes. Esto nos permite asegurar que la única asíntota vertical es \(x = 0\), correspondiente a la única raíz del polinomio del denominador.
Calculamos los límites cuando \(x\to 0\):
$$ \lim_{x \to 0^{+}} \frac{x-1}{x} = - \infty $$
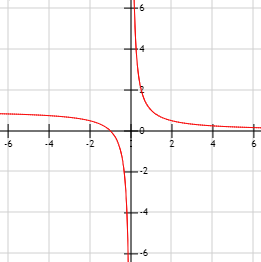
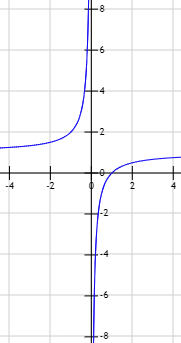
$$ \lim_{x \to 0^{-}} \frac{x-1}{x} = + \infty $$
Gráfica de la función \(f\):
Problema 4
Calcular la asíntota horizontal de la siguiente función en la que el grado del polinomio del denominador es mayor que el del numerador:
$$ f(x) = \frac{x+2}{x^2+2}$$
Solución
Para encontrar las asíntotas horizontales, debemos calcular el límite de la función en los infinitos:
$$ \lim_{x \to + \infty } f(x) = $$
$$ = \lim_{x \to + \infty } \frac{x+2}{x^2+2}= 0$$
Por otro lado,
$$ \lim_{x \to - \infty } f(x) = $$
$$ = \lim_{x \to - \infty } \frac{x+2}{x^2+2}= 0$$
Los límites son 0 precisamente porque el grado del polinomio del denominador es mayor que el del numerador.
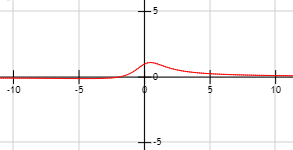
La asíntota horizontal (para ambas ramas de la función) es la recta \(y = 0\).
Gráfica de \(f\):
Problema 5
Calcular la asíntota horizontal de la siguiente función en la que el grado del polinomio del denominador es igual que el grado del polinomio del numerador:
$$ f(x) = \frac{6x-1}{2-3x} $$
Solución
Calculamos el límite en los infinitos:
$$ \lim_{x \to \pm\infty } f(x) = $$
$$ = \lim_{x \to \pm \infty } \frac{6x-1}{2-3x} =$$
$$= \frac{6}{-3}= -2$$
Como el grado de los polinomios es el mismo, el límite es el cociente de los coeficientes directores de los polinomios.
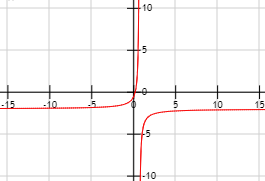
La asíntota horizontal (para ambas ramas) es la recta \(y = -2\).
Gráfica de \(f\):
Problema 6
Comprobar que si \(f\) es la función racional
$$ f(x) = \frac{P(x)}{Q(x)} $$
donde \(P(x)\) y \(Q(x)\) son polinomios sin raíces comunes, entonces:
-
Si el grado de \(Q\) es mayor que el de \(P\), entonces \(y = 0\) es una asíntota horizontal de \(f\).
-
Si el grado \(P\) es mayor que el de \(Q\), entonces \(f\) no tiene asíntota horizontal.
-
Si el grado de \(P\) es \(n\) y es igual que el grado de \(Q\), entonces \(y = a_n/b_n\) es una asíntota horizontal de \(f\) siendo \(a_n\) y \(b_n\) los coeficientes directores de los polinomios \(P\) y \(Q\), respectivamente.
Nota: demostración de dificultad baja.
Solución
La recta \(y=a\) es una asíntota horizontal de \(f\) si
$$ \lim_{x\to \pm \infty} f(x) = a $$
La razón de que los polinomios no tengan raíces comunes es que así la función no puede simplificarse. Si no, podrían cambiar los grados de los polinomios después de simplificar.
Caso a:
Si el grado de \(Q\) es mayor que el de \(P\), entonces el límite existe y es 0. Por tanto, \(y=0\) es una asíntota horizontal.
Caso b:
Si el grado de \(P\) es mayor que el de \(Q\), entonces el límite es \(\pm \infty\) y, por tanto, no hay asíntotas horizontales.
Caso c:
Si los grados son iguales, el límite es igual al cociente de los coeficientes directores:
Supongamos que el grado de \(P\) y el de \(Q\) es el natural \(n\).
Los polinomios son de la forma
$$ P(x) = a_n x^n + a_{n-1}x^{n-1}+…+a_1x + a_0 $$
$$ Q(x) = b_n x^n + b_{n-1}x^{n-1}+…+b_1x + b_0 $$
siendo \(a_n, b_n \neq 0\).
Entonces,
$$ \lim_{x\to \pm \infty} \frac{P(x)}{Q(x)} = \frac{a_n}{b_n} $$
Con lo que la recta \(y = a_n/b_n\) es una asíntota horizontal.
Problema 7
En caso de haberlas, indicar las asíntotas horizontales de las siguientes funciones:
$$ f(x) = \frac{1-x^2}{x^2-2} $$
$$ g(x) = \frac{2x+1}{3x^2-2x} $$
$$ h(x) = \frac{x^7-2}{2x^2+3x} $$
Nota: las expresiones de las funciones están simplificadas.
Solución
Función \(f\):
La función \(f\) tiene la asíntota horizontal \(y = -1\) porque, como los grados de los polinomios son el mismo, el límite en infinito es el cociente de los coeficientes directores.
Gráfica de \(f\):
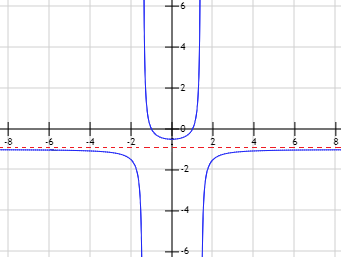
Función \(g\):
La función \(g\) tiene la asíntota horizontal \(y=0\) porque el grado del polinomio del denominador es mayor.
Gráfica de \(g\):
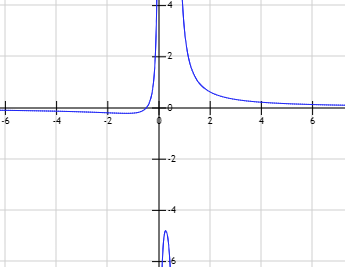
Función \(h\):
La función \(h\) no tiene asíntotas horizontales porque el grado del polinomio del numerador es mayor.
Gráfica de \(h\):
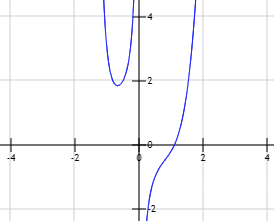
Problema 8
En caso de haberlas, calcular las asíntotas horizontales de las siguientes funciones definidas por partes:
$$ f(x) = \left\{ \begin{array}{l} \frac{3-4x^2}{x^2+x+1} & \mbox{si } x\geq 0 \\ \frac{1}{x+1} & \mbox{si } x< 0\end{array} \right.$$
$$ g(x) = \left\{ \begin{array}{l} \frac{x^2-1}{x} & \mbox{si } x\geq 0 \\ \frac{2x^6-1}{x^5-x^6} & \mbox{si } x< 0\end{array} \right.$$
Solución
Tenemos que calcular los límites de las funciones cuando \(x\) tiende a \(\pm \infty\). Como las funciones están definidas por partes, su expresión cambia cuando calculamos cada uno de los límites.
Función \(f\):
El límite cuando \(x\) tiende a \(+\infty\) es
$$ \lim_{x \to +\infty } f(x) = $$
$$ = \lim_{x \to +\infty } \frac{3-4x^2}{x^2+x+1} = -4$$
El resultado es -4 porque los grados de los polinomios es el mismo.
Por tanto, \(y = -4\) es una asíntota horizontal en la parte de los reales positivos.
El límite cuando \(x\) tiende a \(-\infty\) es
$$ \lim_{x \to -\infty } f(x) = $$
$$ = \lim_{x \to -\infty } \frac{1}{x+1}= 0$$
El resultado es 0 porque el grado del polinomio del denominador es mayor.
Por tanto, \(y = 0\) es una horizontal en la parte de los reales negativos.
Gráfica de \(f\):
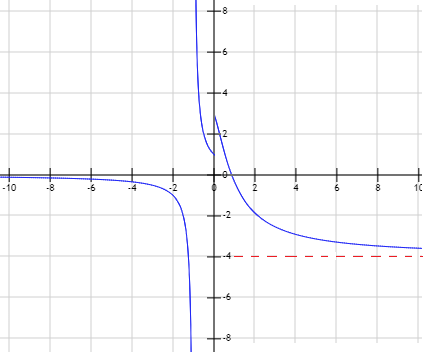
Función \(g\):
El límite cuando \(x\) tiende a \(+\infty\) es
$$ \lim_{x \to +\infty } f(x) = $$
$$ = \lim_{x \to +\infty } \frac{x^2-1}{x} = +\infty$$
En la parte de los reales positivos no hay asíntotas horizontales.
El límite cuando \(x\) tiende a \(-\infty\) es
$$ \lim_{x \to -\infty } f(x) = $$
$$ = \lim_{x \to -\infty } \frac{2x^6-1}{x^5-x^6}= -2$$
En la parte de los reales negativos hay una asíntota horizontal: \(y = -2\).
Gráfica de \(g\):
Problema 9
Calcular la asíntota oblicua de la función
$$ f(x) = \frac{x^2-x^3}{x^2+1} $$
Solución
Como ya sabemos que hay una asíntota oblicua, vamos a calcularla directamente.
La pendiente \(a\) de la asíntota \(y = ax+b\) viene dada por el límite
$$ a= \lim_{x \to \pm\infty } \frac{f(x)}{x} = $$
$$ =\lim_{x \to \pm\infty } \frac{x^2-x^3}{x(x^2+1)}= $$
$$ =\lim_{x \to \pm\infty } \frac{x-x^2}{x^2+1}= -1 $$
Y la ordenada \(b\) es el límite
$$ b= \lim_{x \to \pm\infty } f(x)-ax = $$
$$ =\lim_{x \to \pm\infty } f(x)+x = $$
$$ =\lim_{x \to \pm\infty } = \frac{x^2-x^3}{x^2+1} + x= $$
$$ =\lim_{x \to \pm\infty } = \frac{x^2-x^3 + x^3 +x}{x^2+1} = $$
$$ =\lim_{x \to \pm\infty } = \frac{x^2+x}{x^2+1} = 1$$
Por tanto, la asíntota oblicua es la recta
$$ y = 1 - x$$
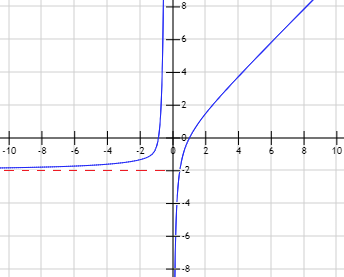
La gráfica de \(f\) es:
Problema 10
Calcular la asíntota oblicua de la función
$$ f(x) = \frac{3-x^2}{2x+2} $$
Solución
La pendiente \(a\) de la asíntota oblicua \(y = ax+b\) viene dada por el límite
$$ a= \lim_{x \to \pm\infty } \frac{f(x)}{x} = $$
$$ =\lim_{x \to \pm\infty } \frac{3-x^2}{x(2x+2)}= $$
$$ =\lim_{x \to \pm\infty } \frac{3-x^2}{2x^2+2x}= -1/2 $$
Y la ordenada \(b\) es el límite
$$ b= \lim_{x \to \pm\infty } f(x)-ax = $$
$$ =\lim_{x \to \pm\infty } f(x)+ \frac{x}{2} = $$
$$ =\lim_{x \to \pm\infty } = \frac{3-x^2}{2x+2} + \frac{x}{2} = $$
$$ =\lim_{x \to \pm\infty } = \frac{3-x^2+x^2+x}{2x+2} = $$
$$ =\lim_{x \to \pm\infty } = \frac{3+x }{2x+2} = \frac{1}{2}$$
Por tanto, la asíntota oblicua es la recta
$$ y = \frac{1-x}{2}$$
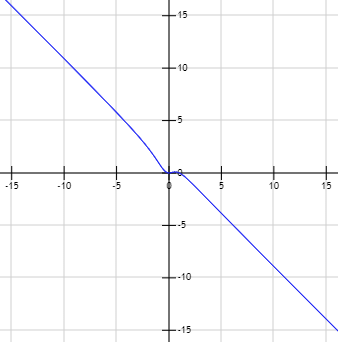
La gráfica de \(f\) es:
Problema 11
Demostrar que la recta \(y=ax+b\) ( con \(a\neq 0\)) es una asíntota oblicua de \(f\) si, y solamente si, existen los límites
$$ \lim_{x \to \pm\infty } \frac{f(x)}{x} = a$$
$$ \lim_{x \to \pm\infty } f(x)-ax = b$$
Nota: demostración de dificultad media.
Solución
Por definición, la recta \(y = ax+b\) es una asíntota oblicua de \(f\) si
$$ \lim_{x \to \pm\infty } f(x) –(ax+b) = 0$$
Supongamos primero que \(y = ax+b\) es una asíntota oblicua y, por tanto, el límite de la definición existe y es 0. Entonces,
$$0 = \lim_{x \to \pm\infty } f(x) –(ax+b) = $$
$$ = \lim_{x \to \pm\infty } f(x) –ax -b $$
Luego
$$ \lim_{x \to \pm\infty } f(x) –ax = b $$
Por el límite anterior,
$$ \lim_{x \to \pm\infty } f(x) –ax = b $$
$$ \lim_{x \to \pm\infty } \frac{f(x) –ax}{x} = 0 $$
$$ \lim_{x \to \pm\infty } \frac{f(x) –ax}{x} + a = a $$
$$ \lim_{x \to \pm\infty } \frac{f(x)}{x} -\frac{ax}{x} + a = a $$
$$ \lim_{x \to \pm\infty } \frac{f(x)}{x} -a + a = a $$
$$ \lim_{x \to \pm\infty } \frac{f(x)}{x} = a $$
Supongamos ahora que existen los dos límites de la definición:
$$ \lim_{x \to \pm\infty } \frac{f(x)}{x} = a$$
$$ \lim_{x \to \pm\infty } f(x)-ax = b$$
Por el segundo límite,
$$0 = \lim_{x \to \pm\infty } f(x)-ax - b = $$
$$ = \lim_{x \to \pm\infty } f(x)-(ax + b)$$
Por tanto, \(y = ax+b\) es asíntota oblicua de \(f\).
Problema 12
Comprobar que si \(f\) es la función racional
$$ f(x) = \frac{P(x)}{Q(x)} $$
donde \(P(x)\) y \(Q(x)\) son polinomios sin raíces comunes de modo que el grado de \(P\) es una unidad mayor que el grado de \(Q\), entonces \(f\) tiene una asíntota oblicua.
Nota: demostración de dificultad alta.
Solución
Por el problema anterior, es suficiente comprobar que existen los límites
$$ \lim_{x \to \pm\infty } \frac{f(x)}{x} = a$$
$$ \lim_{x \to \pm\infty } f(x)-ax = b$$
Si el grado de \(P\) es \(n+1\) y el de \(Q\) es \(n\), los polinomios son de la forma
$$ P(x) = a_{n+1} x^{n+1} + a_n x^n+…+a_1x + a_0 $$
$$ Q(x) = b_n x^n + b_{n-1}x^{n-1}+…+b_1x + b_0 $$
siendo \(a_{n+1}, b_n \neq 0\).
Por tanto, como \(a_{n+1}, b_n \neq 0\),
$$ \lim_{x \to \pm\infty } \frac{f(x)}{x} = $$
$$= \lim_{x \to \pm\infty } \frac{ a_{n+1} x^{n+1} + a_n x^n+…+a_1x + a_0 }{ b_n x^{n+1} + b_{n-1}x^n+…+b_1 x^2 + b_0 x } = \frac{ a_{n+1}}{b_n} = a$$
Ahora tenemos que demostrar que existe el límite
$$ \lim_{x \to \pm\infty } f(x)-ax $$
siendo \(a = a_{n+1} / b_n\).
Operamos en el límite
$$ \lim_{x \to \pm\infty } f(x)-ax =$$
$$ \lim_{x \to \pm\infty } \frac{P(x)}{Q(x)}- ax =$$
$$ = \lim_{x \to \pm\infty } \frac{ a_{n+1} x^{n+1} + a_n x^n+. . . }{ b_n x^n + b_{n-1}x^{n-1}+. . . } -ax= $$
$$ = \lim_{x \to \pm\infty } \frac{ (a_{n+1}-a\cdot b_n) x^{n+1} +(a_n – a\cdot b_{n-1}) x^n +. . . }{ b_n x^n + b_{n-1}x^{n-1}+… } $$
Como \(a = a_{n+1} / b_n\), entonces,
$$ a_{n+1}-a\cdot b_n = a_{n+1}-\frac{ a_{n+1}}{b_n}\cdot b_n = 0$$
Entonces, en el límite anterior tenemos el cociente de dos polinomios del mismo grado. Como \(b_n\neq 0\) por hipótesis, hay dos posibilidades:
-
Si \(b = a_n – a\cdot b_{n-1}\neq 0\), los polinomios tienen el mismo grado y, por tanto, el límite es igual a \(b/b_n\).
-
En caso contrario, el grado del polinomio del denominador es mayor, así que el límite existe y es igual a 0.
En ambos casos, el límite existe.
Problema 13
Encontrar todas las asíntotas de la función
$$ f(x) = \frac{x+2}{x^2-9} $$
Solución
Asíntotas horizontales:
Como el grado del polinomio del denominador es mayor, existe una asíntota horizontal para ambas ramas de \(f\) y es la recta \(y = 0\).
Asíntotas verticales:
El denominador se anula en los puntos \(x = \pm 3\).
Los límites laterales en dichos puntos son:
$$ \lim_{x\to 3^-} f(x) = -\infty $$
$$ \lim_{x\to 3^+} f(x) = +\infty $$
$$ \lim_{x\to -3^-} f(x) = -\infty $$
$$ \lim_{x\to -3^+} f(x) = +\infty $$
Las rectas \(x=-3\) y \(x=3\) son asíntotas verticales.
Asíntotas oblicuas:
Calculamos la pendiente
$$ a = \lim_{x \to \pm\infty } \frac{f(x)}{x} = $$
$$ = \lim_{x \to \pm\infty } \frac{x+2}{x(x^2-9)} = 0 $$
Como obtenemos que la pendiente es 0, no tiene asíntota oblicua (la recta sería \(y = 0\cdot x + b = b\), una recta horizontal).
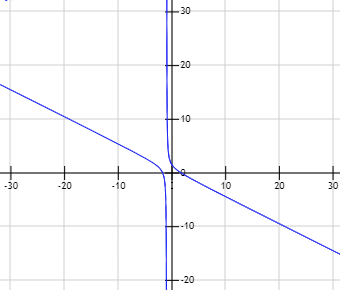
La gráfica de \(f\) es:
Problema 14
Encontrar todas las asíntotas de la función
$$ f(x) = \frac{3x^5-2x}{x^4-5x^2+4} $$
Solución
Asintotas horizontales:
Como el grado del polinomio del numerador es mayor, los límites cuando \(x\) tiende a los infinitos son \(\pm \infty\). Por tanto, no hay asíntotas horizontales.
Asintotas verticales:
Para calcular los puntos que anulan al denominador tenemos que resolver la ecuación bicuadrada.
Sea \(t = x^2\), entonces la ecuación queda como
$$ t^2 – 5t + 4 = 0 $$
Las soluciones son \(t =1\) y \(t = 4\).
Deshacemos el cambio de variable y obtenemos las cuatro raíces:
$$ x^2 = t = 1 \rightarrow x=\pm 1 $$
$$ x^2 = t = 4 \rightarrow x=\pm 2 $$
Por tanto, hay 4 asíntotas verticales: \(x = -1\), \(x=1\), \(x =-2\) y \(x = 2\). En efecto, los límites en dichos puntos son
$$ \lim_{x\to -1} \frac{3x^5-2x}{x^4-5x^2+4} = \pm \infty $$
$$ \lim_{x\to 1} \frac{3x^5-2x}{x^4-5x^2+4} = \pm \infty $$
$$ \lim_{x\to -2} \frac{3x^5-2x}{x^4-5x^2+4} =\pm \infty $$
$$ \lim_{x\to 2} \frac{3x^5-2x}{x^4-5x^2+4} = \pm \infty $$
Asintotas oblicuas:
Como el grado del numerador es mayor que el del denominador en una unidad, sabemos que existe una asíntota oblicua (Problema 12).
Calculamos su pendiente:
$$ a = \lim_{x \to \pm\infty } \frac{f(x)}{x} = $$
$$ = \lim_{x \to \pm\infty } \frac{3x^5-2x}{x(x^4-5x^2+4)} = $$
$$ = \lim_{x \to \pm\infty } \frac{3x^5-2x}{x^5-5x^3+4x} = 3$$
Calculamos su ordenada:
$$ b = \lim_{x \to \pm\infty } f(x) – 3x= $$
$$ = \lim_{x \to \pm\infty } \frac{3x^5-2x}{x^4-5x^2+4} – 3x= $$
$$ = \lim_{x \to \pm\infty } \frac{3x^5-2x -3x^5 +15x^3 -12x}{x^4-5x^2+4} = $$
$$ = \lim_{x \to \pm\infty } \frac{15x^3 -14x}{x^4-5x^2+4} = 0 $$
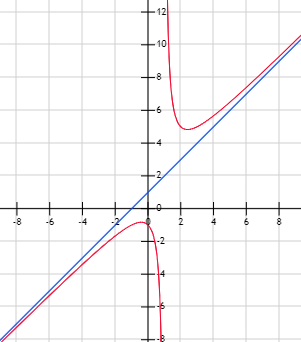
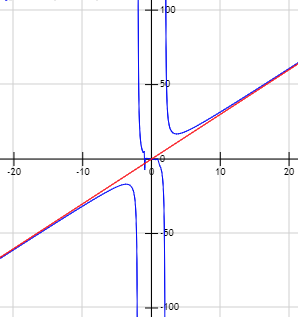
Luego la asíntota oblicua es \(y = 3x\).
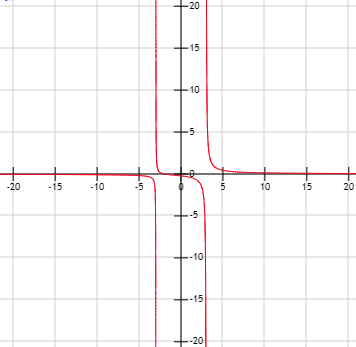
Para poder observar con detalle las asíntotas, vamos a mostrar la gráfica de \(f\) a varias escalas.
La gráfica de \(f\) está representada en azul y las asíntotas en rojo:
Asíntota oblicua:
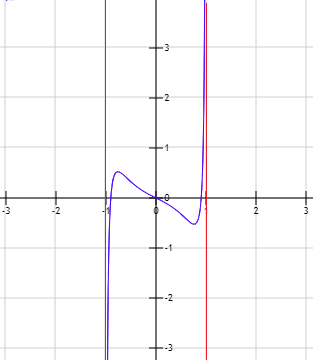
Asíntota verticales \(x=\pm 1\):
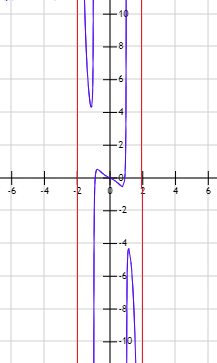
Asíntota verticales \(x=\pm 2\):
Problema 15
Encontrar todas las asíntotas de la función
$$ f(x) = \frac{e^x}{x} $$
Solución
Asíntotas horizontales:
Calculamos los límites en los infinitos:
$$ \lim_{x\to +\infty} \frac{e^x}{x} = +\infty $$
El límite es infinito porque el numerador crece mucho más rápido que el denominador (intuitivamente, podemos pensar que es un caso similar al cociente de polinomios con el grado del numerador mucho mayor). O bien, aplicando L’Hôpital el límite es inmediato.
Sin embargo, el otro límite es:
$$ \lim_{x\to -\infty} \frac{e^x}{x} = 0 $$
Por tanto, existe una asíntota horizontal \(y = 0\) en el lado izquierdo de \(f\).
Asíntotas verticales:
El único punto (finito) candidato para que la función tienda a infinito cuando se le aproxima es el punto \(x = 0\):
$$ \lim_{x\to 0^+} \frac{e^x}{x} = +\infty $$
$$ \lim_{x\to 0^-} \frac{e^x}{x} = -\infty $$
Por tanto, tenemos la asíntota vertical \( x = 0\) por ambos lados.
Asíntotas oblicuas:
Calculamos la pendiente de la asíntota \(y = ax+b\):
$$a = \lim_{x\to \infty } \frac{f(x)}{x} = $$
$$= \lim_{x\to \infty } \frac{e^x}{x^2} = ? $$
El límite sólo existe en el infinito negativo:
$$ \lim_{x\to -\infty } \frac{e^x}{x^2} = 0 $$
En el positivo no existe (no es finito):
$$ \lim_{x\to +\infty } \frac{e^x}{x^2} = +\infty $$
Por tanto, no hay asíntota oblicua porque la pendiente obtenida es 0.
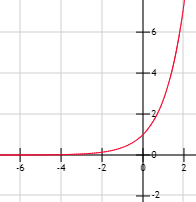
La gráfica de \(f\) es:
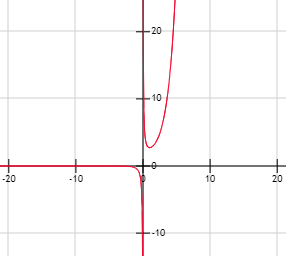


Asíntotas de funciones - © matesfacil.com

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.