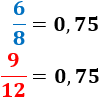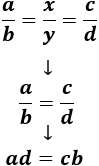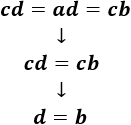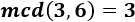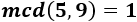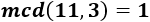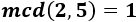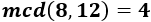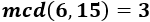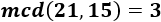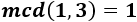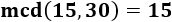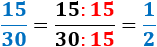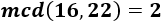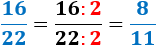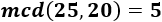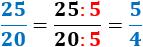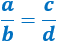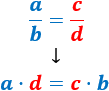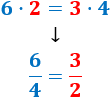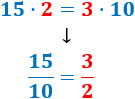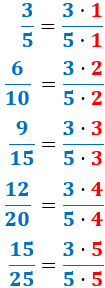Fracción irreducible
En esta página explicamos qué es una fracción irreducible y cómo calcular la fracción irreducible de una fracción. También, demostramos la unicidad de la fracción irreducible.
Contenido de esta página:
- Introducción
- Fracción irreducible de una fracción
- 5 problemas resueltos
Temas relacionados:
Páginas relacionadas
Otras páginas:
Introducción
Recordamos que dos fracciones son equivalentes cuando son fracciones distintas pero representan la misma cantidad, el mismo número o la misma fracción de un todo.
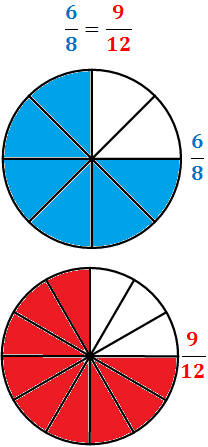
Por ejemplo, las fracciones \(6/8\) (seis octavos) y \(9/12\) (nueve doceavos) son fracciones distintas, pero son equivalentes.
Una fracción \(a/b\) es una fracción irreductible (o irreducible) cuando el máximo común divisor del numerador y del denominador es 1 (\(mcd(a,b)=1\)). Es decir, cuando los números \(a\) y \(b\) son coprimos.
Si una fracción no es irreductible, se dice que es reducible (o reductible).
Por ejemplo, las siguientes fracciones son todas irreductibles:
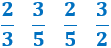
Y las siguientes fracciones son reductibles:
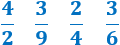
Otra definición:
Dada una fracción de números enteros \(a/b\), se dice que es irreductible si no existe ninguna fracción de enteros \(c/d\) equivalente tal que \( |c|< |a|\) ó \(||d|< |b|\).
Es decir, la fracción es irreductible cuando no existe una fracción equivalente con numerador o denominador menor en módulo.
Fracción irreductible de una fracción
Toda fracción reductible tiene una única fracción irreductible equivalente (con denominador positivo).
Para calcular la fracción irreductible de una fracción, dividimos el numerador y el denominador entre su máximo común divisor.
Por ejemplo, como el máximo común divisor de 18 y 27 es 9, la fracción irreductible de \(18/27\) es la fracción \(2/3\):
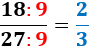
La fracción irreductible de una fracción es única, pero existen fracciones (las equivalentes) con la misma fracción irreductible.
Por ejemplo, la fracción irreductible de \(4/6\) también es \(2/3\).
5 Problemas resueltos
Problema 1
Determinar cuáles de las siguientes fracciones son irreductibles y cuáles son reducibles:
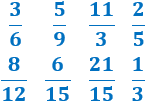
Problema 2
Calcular la fracción irreductible de las siguientes fracciones reducibles:
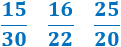
Problema 3
Determinar cuáles de las siguientes fracciones son equivalentes a las fracciones irreductibles \(2/5\) y \(3/2\):
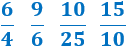
Problema 4
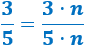
La fracción \(3/5\) es irreductible. Explicar por qué son reducibles todas las fracciones que se obtienen multiplicando el numerador y el denominador de la fracción \(3/5\) por un natural \(n\) mayor que 1.
Problema 5
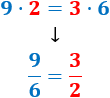
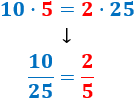
¿Cuál es la relación existente entre las siguientes fracciones? ¿Son fracciones irreductibles?
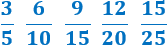
Fracción irreductible - © - matesfacil.com

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.