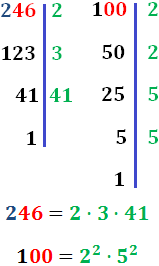
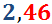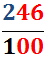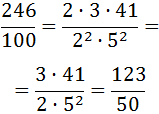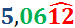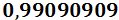Fracción generatriz de números decimales
En esta página recordamos las definiciones de número decimal exacto, periódico puro y periódico mixto y explicamos cómo obtener la fracción generatriz de cada uno de estos tipos de decimales.
Contenido de esta página:
- Introducción
- Decimal exacto
- Decimal periódico puro
- Decimal periódico mixto
- Problemas resueltos
Páginas relacionadas
Otras páginas:
1. Introducción
La fracción generatriz de un número decimal es la fracción irreductible que da como resultado dicho número decimal.
Por ejemplo, el número decimal (periódico puro)
0.428571428571428571428571428571...
tiene período 428571 y está generado por la fracción tres séptimos:
$$ \frac{3}{7} = 0.428571...$$
Nota: recordad que una fracción es irreductible si el máximo común divisor de su numerador y denominador es 1, es decir, si la fracción no se puede simplificar.
Vamos a ver un método para obtener la fracción generatriz para cada unos de los tres tipos de números decimales (exacto, periódico puro y periódico mixto).
Recordatorio:
- la parte entera de un número decimal es el número que hay a la izquierda de la coma,
- y la parte decimal o fraccionaria de un número decimal es el número que hay a la derecha de la coma.
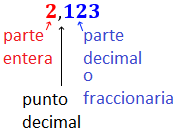
Por ejemplo, la parte decimal de 9,10101010... es 9 y la parte decimal es 10101010...
Notación:
- Los puntos suspensivos detrás de un decimal indican que el número de decimal es infinito.
- El punto decimal lo denotaremos con una coma: ",".