El polinomio \( P_n(f,x_0)\) es una aproximación de
la función \(f\) en el intervalo \(]a,b[\) con un error
que podemos acotar fácilmente.
En esta sección calcularemos los polinomios de Taylor de
orden 2 y de orden 5 de la función exponencial,
mostraremos sus gráficas y acotaremos el error en el intervalo \([0,1]\).
Después, calcularemos el valor de \(cos(0.5)\) con al menos 4 decimales exactos.
Función exponencial
Polinomio de Taylor de orden 2 y de orden 5
de la función exponencial \(f(x) = e^x\) en el punto \(x_0 = 0\):
Las derivadas de la función \( f(x) = e^x \)son:
$$f^{(n)}(x) = e^x, \forall n $$
Por tanto,
$$ f^{(n)}(0) = e^0=1, \forall n$$
El polinomio de orden 5 es
$$P_5(f,0) =1+x+\frac{x^2}{2} +$$
$$ + \frac{x^3}{3!} +\frac{x^4}{4!}+\frac{x^5}{5!}=$$
$$ = 1+x+\frac{x^2}{2} +$$
$$ + \frac{x^3}{6} +\frac{x^4}{24}+\frac{x^5}{120}$$
Y el de orden 2 es
$$P_2(f,0) =1+x+\frac{x^2}{2} $$
Las gráficas de \(f\), de \( P_2(f,0)\) y de \( P_5(f,0)\) son
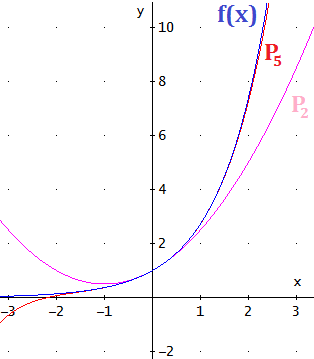
Obsérvese que el error de los polinomios es menor en los
puntos que menos distan de \( x_0 = 0\).
Acotamos el error en el intervalo [0,1]:
En el caso de \(P_2\), el error es
$$f(x)-P_2(f,0) =$$
$$=\frac{f^{(3)}(\xi)}{3!}\cdot x^3 = $$
$$\leq\frac{e^x\cdot x^3}{6}$$
Por tanto,
$$ | f(x)-P_2(f,0)| \leq \frac{e}{6} \simeq 0.45304... $$
Nota: en realidad, en la práctica observamos que en el intervalo
\([0,1]\), el error es menor que 0.22.
En el caso de \(P_5 \), la cota es
$$|f(x)-P_5(f,0)| \leq \frac{e}{5!} \simeq 0.02265$$
Nota: en la práctica, obtenemos que el error es menor
que 0.00162.
Aproximación de \(\cos(0.5)\)
Aproximamos el valor de \(cos(0.5)\) con al
menos 4 decimales exactos.
Utilizaremos un polinomio de Taylor de
orden \( n\) de la función
\( f(x) = cos(x)\) alrededor del
punto \( x_0 = 0\). El orden \(n \) debe ser
suficientemente grande para obtener 4 decimales
exactos, es decir, el error de la
aproximación debe ser menor
que \(0.00001=10^{-5}\).
Existe un punto \( \xi\in [0,0.5]\) tal que
el error del polinomio \( P_n(f, 0)\) es
$$E=\left|\frac{f^{(n+1)}(\xi)}{(n+1)!}(0.5)^{n+1}\right|$$
Las derivadas de \(f(x)=cos(x)\) son el seno y el
coseno. Tendremos en cuenta que
$$ |cos(x)|, |sin(x)|\leq 1, \forall x$$
Exigimos que el error sea menor
que \(10^{-5}\) para obtener el
orden \(n\) que se requiere:
$$E\leq \left|\frac{0.5^{n+1}}{(n+1)!}\right| \leq 10^{-5} $$
Por tanteo, debe escogerse un \(n \geq 6\).
El polinomio de Taylor de orden 6 de \(f\) es
$$ P_6(f,0) (x)= 1-\frac{x^2}{2} +$$
$$ + \frac{x^4}{24} - \frac{x^6}{720} $$
Evaluando el polinomio en 0.5, obtenemos
$$cos(0.5) = P_6(f,0) (0.5) = $$
$$=\frac{40439}{46080}\simeq 0.8775824652$$
Nota: en realidad, la aproximación tiene 6 decimales
exactos.
Nota 2: como \(sin(0) = 0\), se tiene que
\( P_4(f,0) = P_5(f,0)\). Por tanto, el error cometido por
ambos polinomios es el mismo, obteniéndose 3 decimales exactos. Por
ello debe utilizarse \( n\geq 6\) y esto hace que el error disminuya
drásticamente (por el factorial del denominador).



