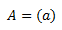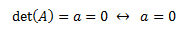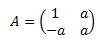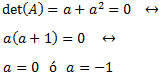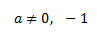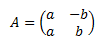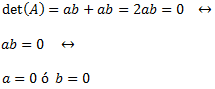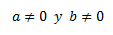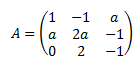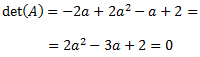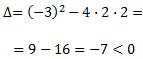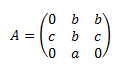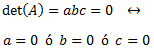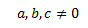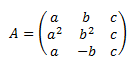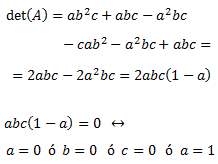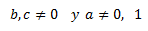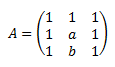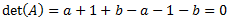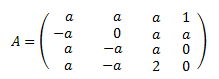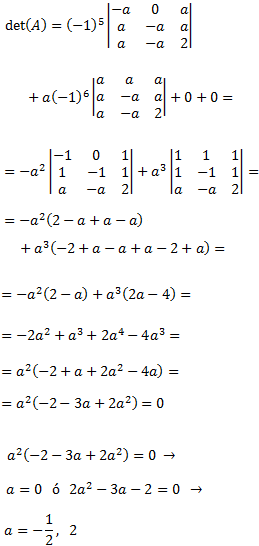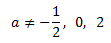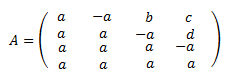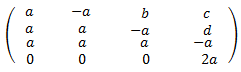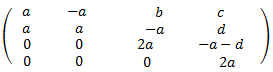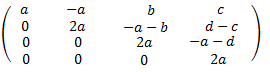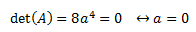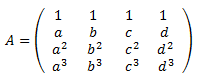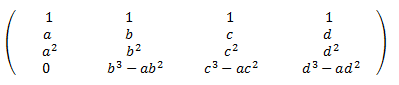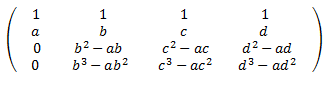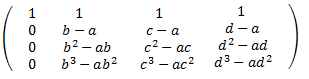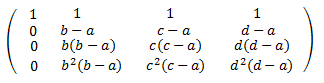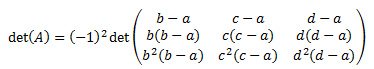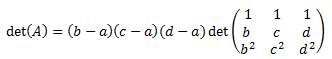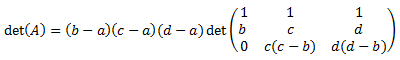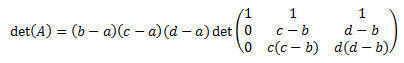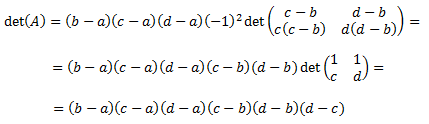En todos los problemas deben determinarse los valores de los parámetros para que las matrices sean invertibles.
Problema 1
Matriz de dimensión 1x1
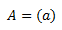
Ver solución
El determinante de una matriz de dimensión 1x1 es el único elemento de la matriz: \(|A|=a\). Por tanto, la matriz es regular si \(a\neq 0\):
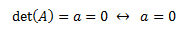
Problema 2
Matriz de dimensión 2x2
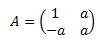
Ver solución
El determinante de una matriz 2x2 es la resta del producto de los elementos de sus diagonales:
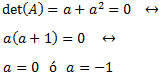
Por tanto, la matriz es regular cuando
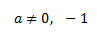
Problema 3
Matriz de dimensión 2x2
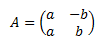
Ver solución
Calculamos el determinante e igualamos a 0:
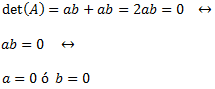
Por tanto, la matriz es regular cuando
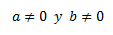
Problema 4
Matriz de dimensión 3x3
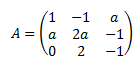
Ver solución
Calculamos el determinante por la regla de Sarrus y lo igualamos a 0:
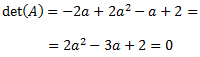
Tenemos una ecuación de segundo grado cuyo discriminante es
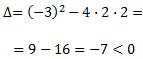
Como es negativo, la ecuación no tiene soluciones reales y por tanto, el determinante será siempre distinto de 0 (considerando que \(a\) y \(b\) son reales).
Luego la matriz es siempre regular.
Problema 5
Matriz de dimensión 3x3
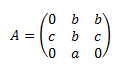
Ver solución
Calculamos el determinante e igualamos a 0:
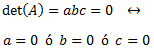
Por tanto, la matriz es regular cuando
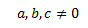
Problema 6
Matriz de dimensión 3x3
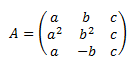
Ver solución
Calculamos el determinante e igualamos a 0:
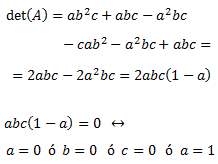
Hemos escrito la ecuación en forma factorizada. Como tenemos un producto, éste es 0 cuando alguno de los factores es 0, lo cual ocurre cuando alguno de los parámetros es 0 o bien, cuando \(a = 1\).
Por tanto, la matriz es regular cuando ninguno de los parámetros es 0 y \(a\neq 1\):
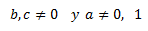
Problema 7
Matriz de dimensión 3x3
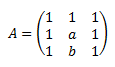
Ver solución
El determinante de la matriz es siempre 0, independientemente de los valores de los parámetros:
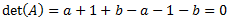
La matriz nunca es regular. Es singular siempre.
Problema 8
Matriz de dimensión 4x4
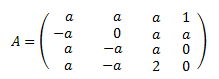
Ver solución
La matriz es de dimensión 4x4, por lo que tendremos que desarrollar el determinante mediante la fórmula de Laplace.
Como tenemos dos 0's en la última columna, desarrollaremos el determinante por dicha fila para que el desarrollo sea más rápido.
Aplicaremos también las propiedades de los determinantes (segunda igualdad) para extraer factores del determinante.
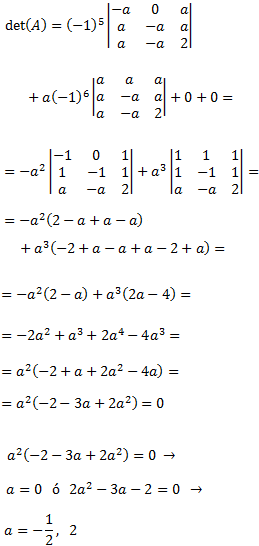
Por tanto, la matriz es regular cuando
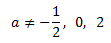
Problema 9
Matriz de dimensión 4x4
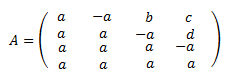
Ver solución
Ni siquiera nos plantemos aplicar la fórmula de Laplace porque es muy rápido obtener la forma escalonada de la matriz. Usaremos las propiedades de los determinantes.
Recordad que podemos sumar a una fila otra fila multiplicada por un escalar sin que cambie el determinante.
Le restamos a la fila 4 la fila 3:
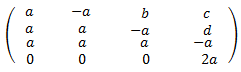
Le restamos a la fila 3 la fila 2:
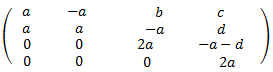
Le restamos a la fila 2 la fila 1:
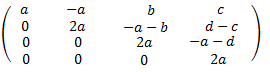
Tenemos una matriz triangular, con lo que el determinante es el producto de los elementos de la diagonal
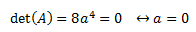
Por tanto, la matriz es regular cuando \(a\neq 0\).
Problema 10
Matriz de dimensión 3x3
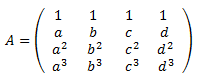
Ver solución
Si no aplicamos las propiedades de los determinantes, obtendremos una expresión de 2 ó 3 líneas.
Primero, vamos a realizar operaciones elementales fila.
Le restamos a la fila 4 la fila 3 multiplicada por \(a\):
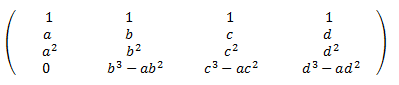
Le restamos a la fila 3 la fila 2 multiplicada por \(a\):
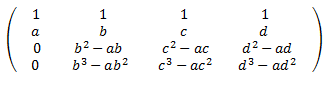
Le restamos a la fila 2 la fila 1 multiplicada por \(a\):
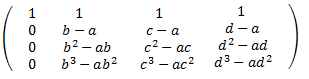
Reescribimos la matriz (factor común):
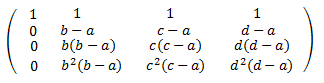
Desarrollamos el determinante por Laplace por la columna 1:
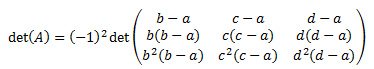
Aplicamos propiedades del determinante: el determinante multiplicado por un escalar no nulo es el determinante de la matriz con una fila (o columna) multiplicada por dicho escalar:
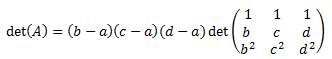
Le restamos a la fila 3 la fila 2 multiplicada por \(b\):
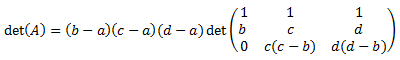
Le restamos a la fila 2 la fila 1 multiplicada por \(b\):
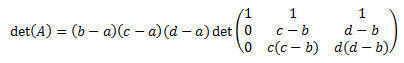
Desarrollamos el determinante por Laplace por la columna 1
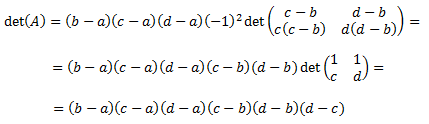
Por tanto, la matriz es regular si todos los parámetros son distintos entre sí.


Determinantes de matrices con parámetros -
© -
matesfacil.com

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.