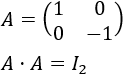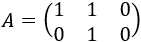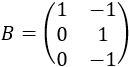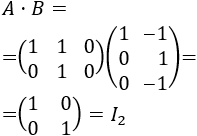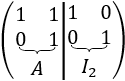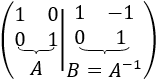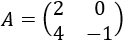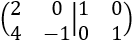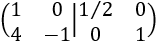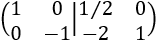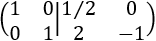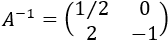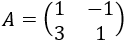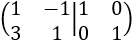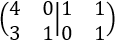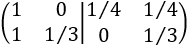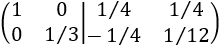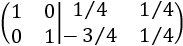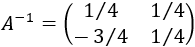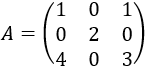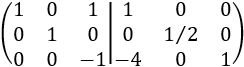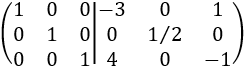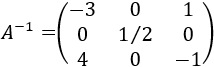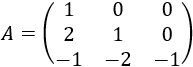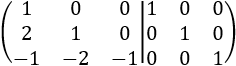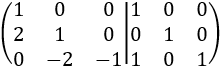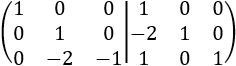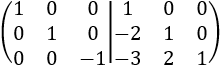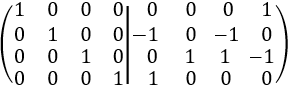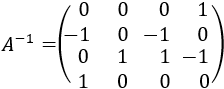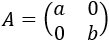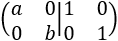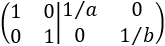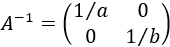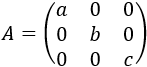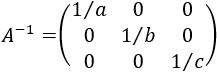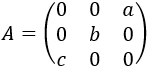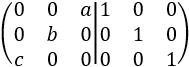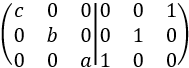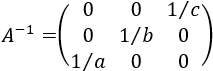Llamaremos operaciones elementales fila (sobre una matriz) a las siguientes operaciones:
-
Multiplicar una fila por un número distinto de 0.
-
Sumar (o restar) a una fila, el múltiplo de otra fila.
-
Intercambiar el orden de las filas.
Recordad que, si una matriz cuadrada es regular, entonces podemos realizar un número finito de operaciones elementales fila para transformar la matriz en la matriz identidad.
En el método de Gauss se realizan las mismas operaciones sobre la matriz identidad, transformándose así en la matriz inversa de \(A\).
Los pasos del método de Gauss son:
-
Escribimos una matriz doble que contiene a la matriz \(A\) en un lado y a la matriz identidad en el otro. Por ejemplo,
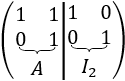
-
Realizamos operaciones elementales fila para transformar la matriz \(A\) en la identidad. En el ejemplo, es suficiente restar la fila 2 a la fila 1:
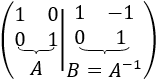
-
Al terminar, por lo que dijimos anteriormente, la matriz \(B\) del lado derecho es, precisamente, la inversa de \(A\): \(B=A^{-1}\).
En todos los problemas debe hallarse la matriz inversa mediante el método de Gauss.
Problema 1
Matriz de dimensión 2x2
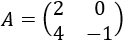
Ver solución
La matriz por bloques es
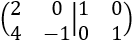
Dividimos la fila 1 entre 2:
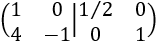
A la fila 2 le restamos el cuádruple de la fila 1:
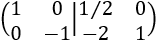
Multiplicamos la fila 2 por -1:
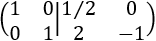
Como tenemos la identidad en el lado izquierdo, la inversa de \(A\) es la matriz del lado derecho:
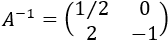
Problema 2
Matriz de dimensión 2x2
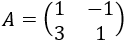
Ver solución
La matriz por bloques es
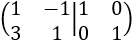
Sumamos la fila 2 a la fila 1:
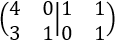
Dividimos la fila 1 entre 4 y la fila 2 entre 3:
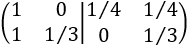
Restamos la fila 1 a la fila 2:
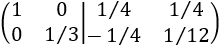
Multiplicamos la fila 2 por 3:
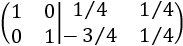
Por tanto, la inversa de \(A\) es
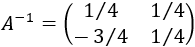
Problema 3
Matriz de dimensión 3x3
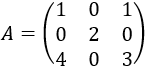
Ver solución
La matriz por bloques es
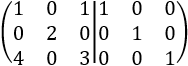
La fila 2 la dividimos entre 2. Le restamos a la fila 3 el cuádruple de la fila 1:
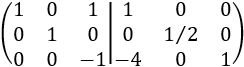
Sumamos la fila 3 a la fila 1. Después, multiplicamos la fila 3 por -1:
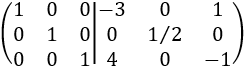
Como ya tenemos la identidad en el lado izquierdo, hemos terminado. Por tanto, la matriz inversa de \(A\) es
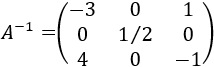
Problema 4
Matriz de dimensión 3x3
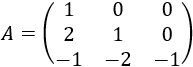
Ver solución
La matriz por bloques es
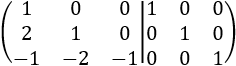
Sumamos la fila 1 a la fila 3:
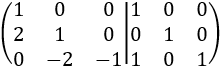
Restamos el doble de la fila 1 a la fila 2:
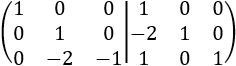
Sumamos el doble de la fila 2 a la fila 3:
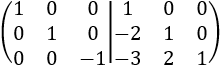
Multiplicamos la fila 3 por -1:
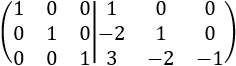
Por tanto, la inversa de \(A\) es
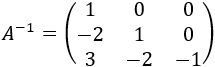
Problema 5
Matriz de dimensión 4x4
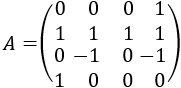
Ver solución
La matriz por bloques es
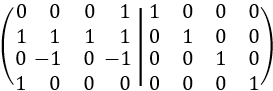
Cambiamos la fila 1 por la fila 4:
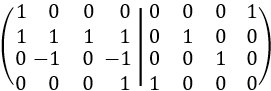
Sumamos la fila 3 a la fila 2:

Restamos la fila 1 a la fila 2 y sumamos la fila 4 a la fila 3:
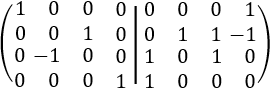
Cambiamos la fila 2 por la fila 3:
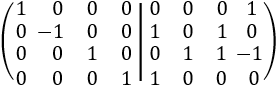
Multiplicamos la fila 2 por -1:
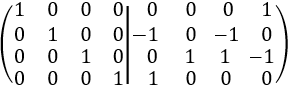
Por tanto, la inversa de \(A\) es
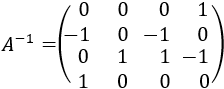
Problema 6
Matriz diagonal de dimensión 2x2 (\(a\) y \(b\) son distintos de 0)
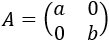
Ver solución
Veremos que la inversa de una matriz diagonal es una matriz diagonal cuyos elementos son los inversos.
La matriz por bloques es
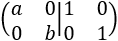
Como \(a\neq0\) y \(b\neq 0\), dividimos la fila 1 entre \(a\) y la fila 2 entre \(b\):
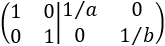
Por tanto, la inversa de \(A\) es
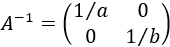
Problema 7
Matriz diagonal de dimensión 3x3 (\(a\), \(b\) y \(c\) son distintos de 0)
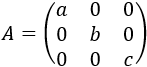
Ver solución
Dividiendo las filas 1, 2, y 3 entre \(a\), \(b\) y \(c\), respectivamente, tenemos que la inversa de \(A\) es
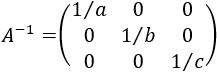
Problema 8
Matriz diagonal secundaria de dimensión 3x3 (\(a\), \(b\) y \(c\) son distintos de 0)
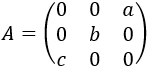
Ver solución
La matriz por bloques es
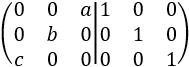
Tenemos que cambiar el orden de las filas 2 y 3 y dividir entre \(a\), \(b\) y \(c\).
Cambiamos el orden:
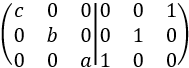
Dividiendo las filas 1, 2, y 3 entre \(c\), \(b\) y \(a\), respectivamente, tenemos que la inversa de \(A\) es
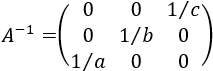


Cálculo de la matriz inversa mediante Gauss -
© matesfacil.com

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.