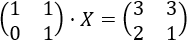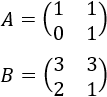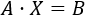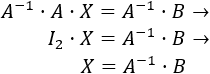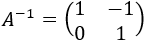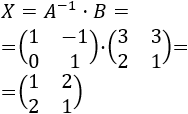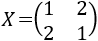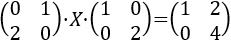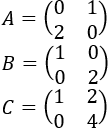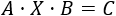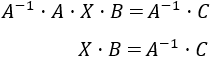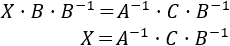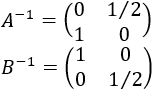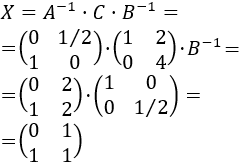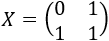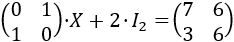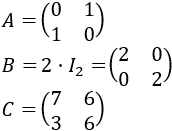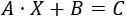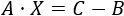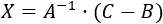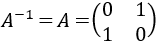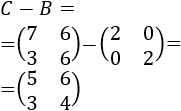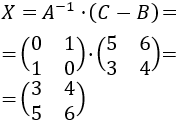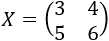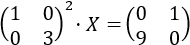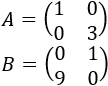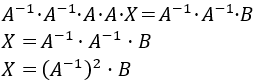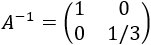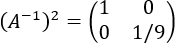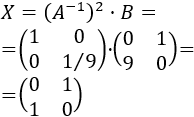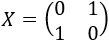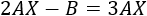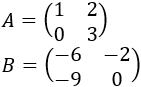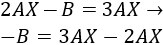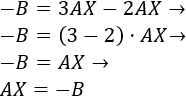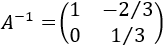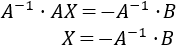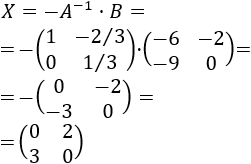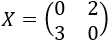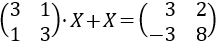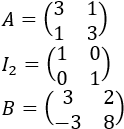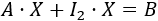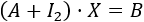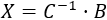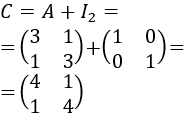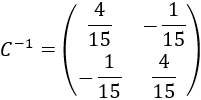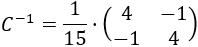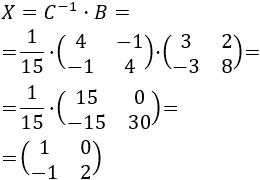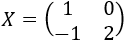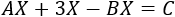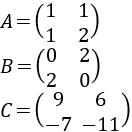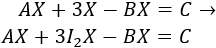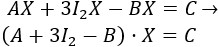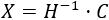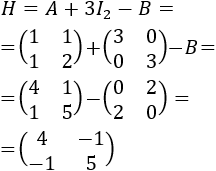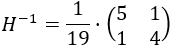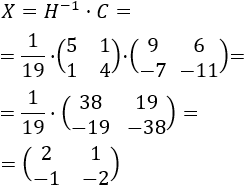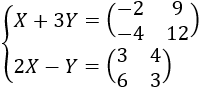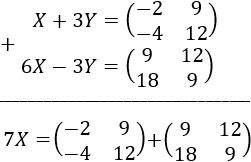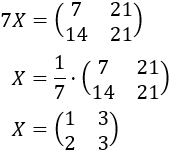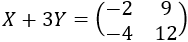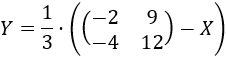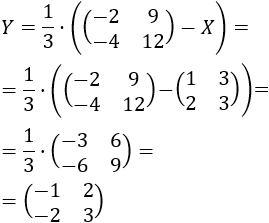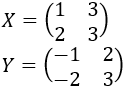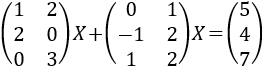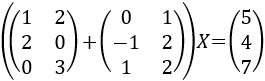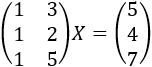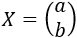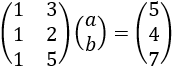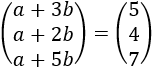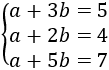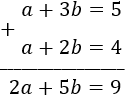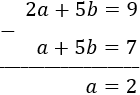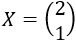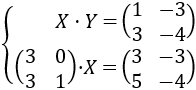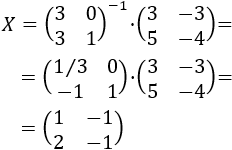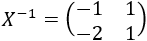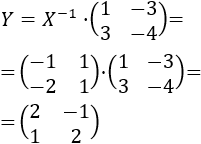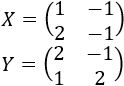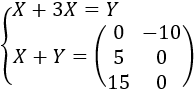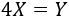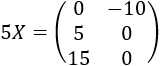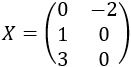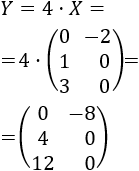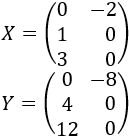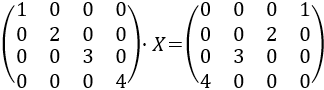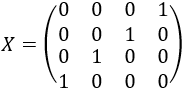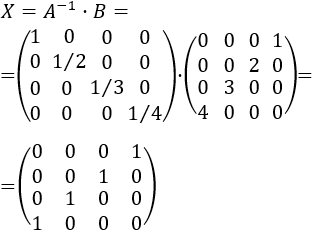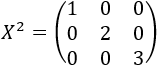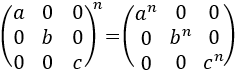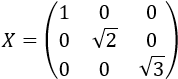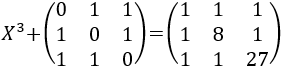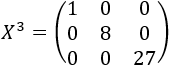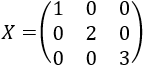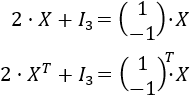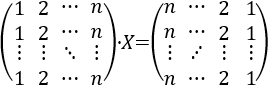Notación:
-
Para abreviar, diremos postmultiplicar y premultiplicar para referirnos a multiplicar por una matriz por la derecha y por la izquierda, respectivamente.
-
Denotaremos la matriz identidad de dimensión \(n\) como \(I_n\).
-
No siempre escribiremos el punto · de la multiplicación.
Puede resultaros útil la calculadora online de la matriz inversa.
Problema 1
Resolver la siguiente ecuación matricial:
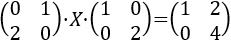
Ver solución
Sean las matrices
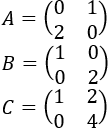
La ecuación que tenemos es
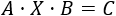
Si las matrices \(A\) y \(B\) son invertibles (regulares), premultiplicamos por la inversa de \(A\) para despejar la incógnita:
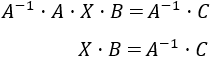
Postmultiplicamos también por la inversa de \(B\):
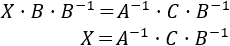
Las inversas de \(A\) y de \(B\) son
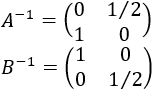
Calculamos la incógnita:
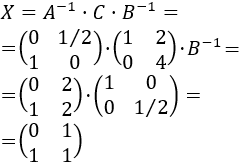
Por tanto, la solución es
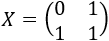
Problema 2
Resolver la siguiente ecuación matricial:
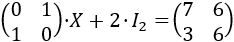
siendo \(I_2\) la matriz identidad de dimensión 2.
Ver solución
Sean las matrices
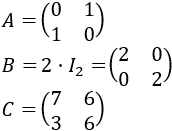
La ecuación que tenemos es
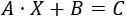
Pasando \(B\) al otro lado,
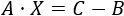
Premultiplicando por la inversa de \(A\),
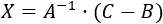
Calculamos la inversa de \(A\):
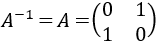
La resta de matrices del lado derecho es
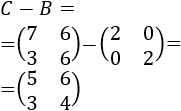
Calculamos \(X\):
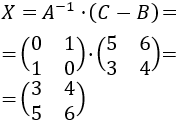
Por tanto, la solución de la ecuación matricial es
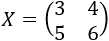
Problema 3
Resolver la siguiente ecuación matricial:
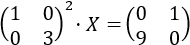
Ver solución
Sean las matrices
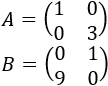
Ambas matrices son regulares. Premultiplicamos dos veces por la inversa de \(A\):
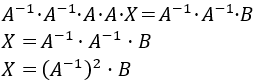
Calculamos la inversa de \(A\) (como es diagonal, su inversa es diagonal con los inversos de \(A\)):
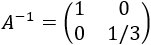
Calculamos su cuadrado (como es diagonal, el resultado es elevar al cuadrado sus elementos):
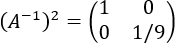
Finalmente, la postmultiplicamos por \(B\):
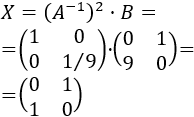
Por tanto, la solución de la ecuación matricial es
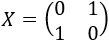
Problema 4
Resolver la siguiente ecuación matricial:
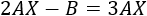
siendo
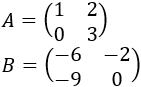
Ver solución
Podemos pasar el \(2AX\) al lado derecho:
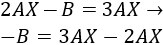
Utilizamos la propiedad distributiva del producto de matrices respecto de la suma:
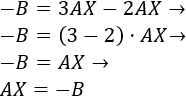
La matriz \(A\) es invertible porque su determinante es 3. Su inversa es
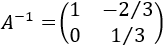
Premultiplicamos la ecuación por la inversa de \(A\):
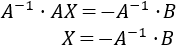
Calculamos la incógnita \(X\):
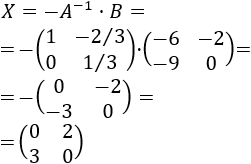
Por tanto, la solución de la ecuación matricial es
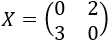
Problema 5
Resolver la siguiente ecuación matricial:
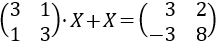
Ver solución
Sean las matrices
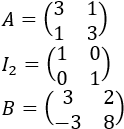
Entonces, la ecuación que tenemos es
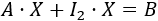
Como el producto de matrices es distributivo respecto de la suma, podemos escribir la ecuación como
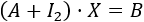
Si la matriz \(C=A+I_2\) tiene inversa, entonces la solución de la ecuación matricial es
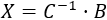
Calculamos la matriz \(C\) y su inversa, si la tiene:
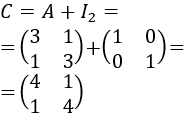
El determinante de \(C\) es no nulo, así que tiene inversa y es
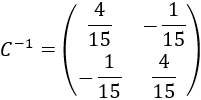
Para facilitar los cálculos, podemos escribir la matriz como
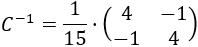
Calculamos la incógnita \(X\):
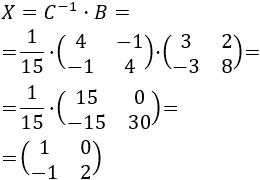
Por tanto, la solución de la ecuación matricial es
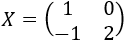
Problema 6
Resolver la siguiente ecuación matricial:
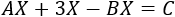
siendo
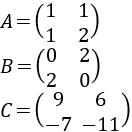
Ver solución
Podemos escribir la matriz identidad en el segundo sumando:
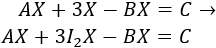
Como el producto de matrices es distributivo respecto de la suma,
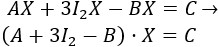
Sea la matriz \(H = A+3I_2-B\). Si \(H\) es regular, podemos calcular \(X\) premultiplicando por su inversa a \(C\):
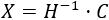
Calculamos la matriz \(H\):
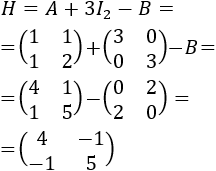
La inversa de \(H\) es
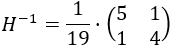
Calculamos la incógnita \(X\):
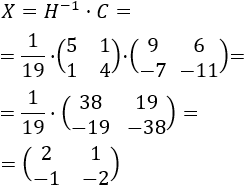
Problema 7
Resolver el siguiente sistema de ecuaciones matriciales:
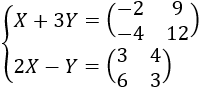
Ver solución
Resolvemos por reducción.
A la primera fila le sumamos el triple de la segunda para obtener una ecuación con una sola incógnita:
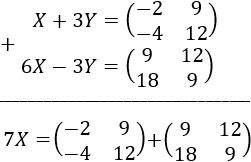
Ya podemos calcular la matriz \(X\):
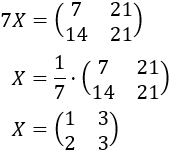
Volvemos a la primera ecuación:
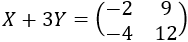
Despejamos la matriz \(Y\):
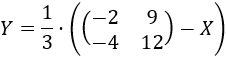
Sustituimos la matriz \(X\) en la ecuación:
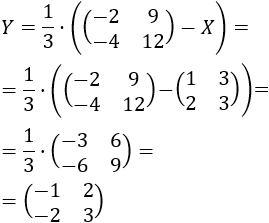
Por tanto, la solución del sistema de ecuaciones matriciales es
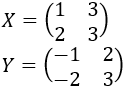
Problema 8
Resolver la siguiente ecuación matricial:
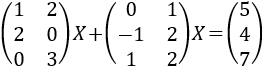
Ver solución
Utilizando la propiedad distributiva del producto de matrices respecto de la suma, podemos escribir la ecuación como
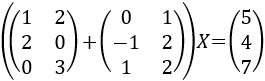
Sumamos las matrices del lado izquierdo:
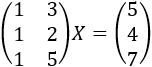
Como la matriz del lado izquierdo no es cuadrada, no podemos resolver la ecuación multiplicando por su inversa.
La dimensión de la matriz del lado izquierdo es 3x2 y la del lado derecho es 3x1. Por tanto, la matriz incógnita es de dimensión 2x1, así que tiene la forma
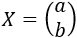
Sustituyendo en la ecuación,
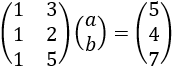
Calculamos el producto:
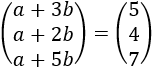
Tenemos tres ecuaciones y dos incógnitas:
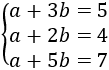
Sumamos las dos primeras ecuaciones obteniendo
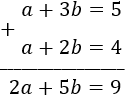
A esta ecuación le restamos la última:
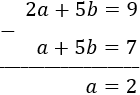
Una vez tenemos \(a=2\), fácilmente se calcula \(b=1\).
Por tanto, la solución de la ecuación matricial es
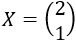
Problema 9
Resolver el siguiente sistema de ecuaciones matriciales:
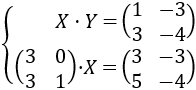
Ver solución
Como la matriz del lado izquierdo de la segunda ecuación es invertible, podemos calcular \(X\). Si \(X\) es también invertible, podemos calcular \(Y\) premultiplicando por \(X^{-1}\) en la primera ecuación.
Calculamos \(X\):
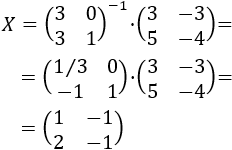
La matriz \(X\) tiene inversa y es
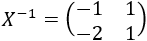
Calculamos \(Y\):
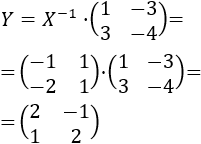
Por tanto, la solución del sistema de ecuaciones matriciales es
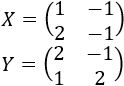
Problema 10
Resolver el siguiente sistema de ecuaciones matriciales:
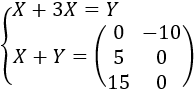
Ver solución
De la primera ecuación tenemos
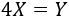
Sustituyendo en la segunda,
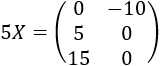
Por tanto, la matriz \(X\) es
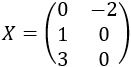
Calculamos la matriz \(Y\):
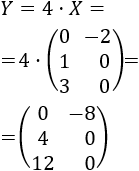
Por tanto, la solución del sistema de ecuaciones matriciales es
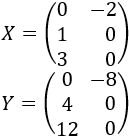
Problemas para pensar:
Problema 11
Resolver la siguiente ecuación matricial:
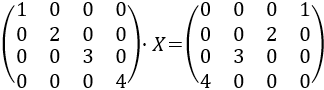
Ver solución
Llamamos \(A\) a la matriz del lado izquierdo y \(B\) a la del derecho.
La matriz \(X\) cambia el orden de los elementos de las filas de \(A\) al postmultiplicarla. Esta matriz es como la identidad, pero con la diagonal hacia el otro lado:
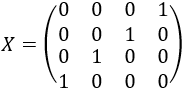
Podéis comprobarlo calculando la inversa de \(A\) y multiplicando por \(B\).
La inversa de una diagonal es la matriz diagonal con los inversos:

La multiplicamos por \(B\):
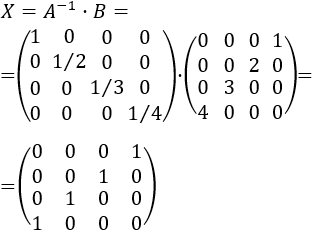
Problema 12
Resolver la siguiente ecuación matricial:
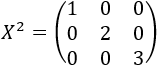
Ver solución
La forma más rápida de resolver esta ecuación es aprovechar la propiedad de las potencias de matrices cuadradas diagonales:
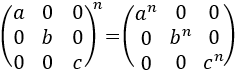
La hemos escrito para dimensión 3, pero es para todas las dimensiones.
Por tanto, una solución de la ecuación matricial es
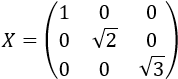
Si cambiamos algunos o todos los signos de los elementos de la diagonal de la matriz \(X\), sigue siendo solución de la ecuación.
Problema 13
Resolver la siguiente ecuación matricial:
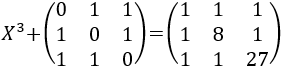
Ver solución
Restando matrices, tenemos que \(X^3\) es diagonal:
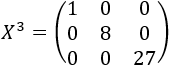
Por lo que dijimos en el problema anterior, la única solución de la ecuación matricial es
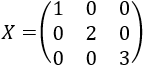
Problema 14
¿Están bien planteadas las siguientes dos ecuaciones matriciales? Justificar la respuesta.
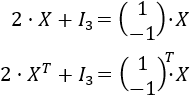
\(T\) significa trasposición de matrices.
Ver solución
En la primera ecuación, si el producto de la derecha se puede calcular es porque la matriz \(X\) tiene 1 fila. Sin embargo, para poder sumar la identidad de dimensión 3 a la matriz \(2·X\), ésta tiene que tener 3 filas.
En la segunda ecuación, razonando del mismo modo, la matriz \(X\) tiene que tener 2 filas, así que su traspuesta no se puede sumar con la identidad de dimensión 3.
Problema 15
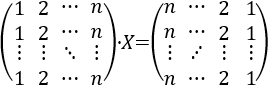
donde:
-
Las matrices son cuadradas de dimensión \(n\).
-
La matriz de la izquierda tiene en la posición \((i,j)\) el número \(j\).
-
La matriz de la derecha tiene en la posición \((i,j)\) el número \(n-j+1\).
Ver solución
La incógnita \(X\) es la matriz que cambia el orden de las columnas de una matriz al multiplicarla. Ya vimos esta matriz en el Problema 11:

Es decir, es la matriz de 0's con diagonal secundaria de 1's.


Ecuaciones matriciales y sistemas de ecuaciones matriciales -
© matesfacil.com

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.