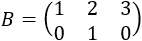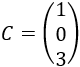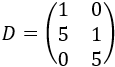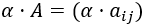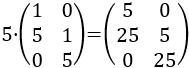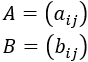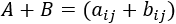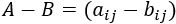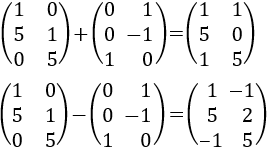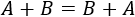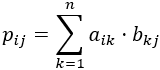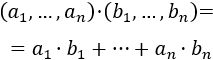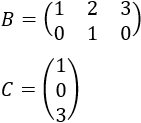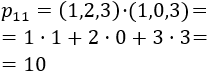Introducción a las matrices

Contenido de esta página:

1. Definición de matriz
2. Producto por un escalar
3. Suma y resta de matrices
4. Producto de matrices

Una matriz es un objeto matemático. Informalmente, podemos decir que una matriz es como una tabla de números. Tiene filas y columnas y la posición de cada número es relevante.

La dimensión de una matriz es \(nxm\), siendo \(n\) el número de filas y \(m\) el de columnas.

Ejemplo:

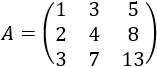
La matriz \(A\) tiene 3 columnas y 3 filas, así que su dimensión es 3x3.

• La fila 1 de la matriz es 1, 3, 5.
• La fila 3 de la matriz es 3, 7, 13.
• La columna 2 de la matriz es 3, 4, 7.
• La columna 3 de la matriz es 5, 8, 13.

Nos referimos a la posición de un número de la matriz \(A\) como \((i,j)\), donde \(i\) es el número de la fila a la que pertenece y \(j\) el de la columna.

Por ejemplo,

• El número de la posición \((1,3)\) de la matriz \(A\) es 5.
• El número de las posiciones \((1,2)\) y \((3,1)\) es 3.
• El número de la posición \((3,3)\) es 13.

Por ejemplo, los elementos de la diagonal de \(A\) son 1, 4, 13.

Para hablar de una matriz de forma genérica, suele utilizarse \(a_{i,j}\) ó \(a_{ij}\) para denotar al elemento de la posición \((i,j)\) de una matriz. Por ejemplo,

Con esta notación, solemos referirnos a una matriz \(A\) como

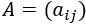
Finalmente, diremos que los elementos de una matriz pueden ser números reales, complejos u otros elementos matemáticos, elementos de un cuerpo \(K\) en general.

Sea una matriz \(A=(a_{ij})\) sobre un cuerpo \(K\), es decir, \(a_{ij}\in K\) (como \(K = \mathbb{R}\)). Se define el producto de un escalar \(\alpha \in K\) por la matriz \(A\) como

Es decir,

El producto de un escalar por una matriz es conmutativo porque el producto de escalares de un cuerpo \(K\) lo es:

$$ \alpha ·A = A·\alpha $$

Es decir, si las matrices son

• La suma \(A+B\) es

  

• La resta \(A-B\) es

  

Obviamente, la matriz resultante tiene la misma dimensión que las matrices \(A\) y \(B\).

Más ejemplos en suma y trasposición de matrices.

Propiedades de la suma de matrices:

• Conmutativa:

  

• Asociativa:

  

• El producto por un escalar es distributivo respecto de la suma (y resta) de matrices:

  

El producto de matrices es un poco más complejo.

Sean las matrices \(A=(a_{ij})\) de dimensión \(mxn\) y \(B=(b_{ij})\) de dimensión \(nxp\) (el número de columnas de \(A\) y el de filas de \(B\) debe coincidir).

Entonces, se define el producto matricial \(A·B\) (o, simplemente, \(AB\)) como la matriz de dimensión \(mxp\) cuyo elemento en la posición \((i,j)\) es

Es decir,

Recordad que el producto escalar de dos vectores es

Más ejemplos en producto de matrices.

Propiedades del producto matricial:

• No es, generalmente, conmutativo. Por ejemplo,

  

• Propiedad asociativa:

  

• Propiedad distributiva respecto de la suma (por la derecha y por la izquierda):

  

• La matriz identidad de dimensión correspondiente es el neutro del producto por uno u otro lado. Si \(A\) es de dimensión \(mxn\),

  

  Recordad que \(I_n\) es la matriz de dimensión \(nxn\) formada por 1's en la diagonal y 0's en las otras posiciones.

  Si la matriz \(A\) es cuadrada de dimensión \(nxn\),

  

• Si la matriz \(A\) es de dimensión \(nxn\) y es regular, existe una matriz \(A^{-1}\) (matriz inversa de \(A\)) tal que

  

---