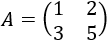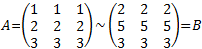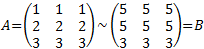Matrices Equivalentes

Contenido de esta página:

1. Introducción
2. Operaciones elementales fila
3. Equivalencia entre matrices
4. Forma escalonada de una matriz
5. Forma escalonada reducida de una matriz

Vamos a explicar por qué, entre otras razones, es tan importante la relación de equivalencia entre matrices.

Recordad que un sistema de ecuaciones lineales se puede representar en forma matricial como

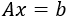
donde

• \(A\) es la matriz de coeficientes de las incógnitas,
• \(x\) es la matriz columna con las incógnitas,
• \(b\) es la matriz columna con los términos independientes de las ecuaciones.

De hecho, podemos representar el sistema \(AX=b\) con una sola matriz: \(A^*\), llamada matriz ampliada o aumentada del sistema:

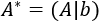
La matriz ampliada es una matriz por bloques: contiene a la matriz \(A\) en el lado izquierdo y a la matriz \(b\) en el derecho.

Por ejemplo, consideremos el sistema de ecuaciones

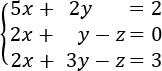
Su matriz ampliada es

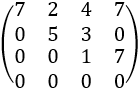
Consideremos ahora la matriz ampliada siguiente:

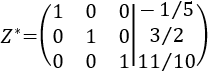
Es la matriz ampliada del sistema

Supongamos cierto el siguiente teorema:

Entonces, si las matrices ampliadas \(A^*\) y \(Z^*\) son equivalentes (lo son), entonces ya tenemos la solución del sistema asociado a la matriz \(A^*\):

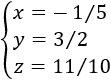
Por tanto, si demostramos el teorema anterior (*), una forma de resolver un sistema con matriz ampliada \(A^*\) es hallar una matriz equivalente que nos proporcione rápidamente la solución del sistema, como \(Z^*\).

Este método de resolver un sistema es el método de Gauss y el de Gauss-Jordan (son variantes del mismo). Podéis encontrar ejemplos del método en:

Eliminación de Gauss y de Gauss-Jordan

Más adelante, vamos a definir como matrices equivalentes a la matriz \(A\) a las matrices que se obtienen al realizar una o más operaciones elementales fila sobre \(A\).

Dada una matriz \(A\), las operaciones elementales fila son:

En cada una de las operaciones anteriores hemos definido una matriz (\(E^s (a)\), \(E^s _r (a)\) y \(E^{s,r}\)). Estas matrices se denominan matrices elementales. Si multiplicamos una de estas matrices por la matriz \(A\), se obtiene la matriz resultante al aplicar a \(A\) la operación elemental fila asociada a dicha matriz.

Por ejemplo, la matriz \(E^{s,r}·A\) es la matriz \(A\) con las filas \(s\) y \(r\) intercambiadas.

Diremos que una matriz tiene forma escalonada si se cumplen las siguientes condiciones:

Dicho en otras palabras, podemos transformar cualquier matriz en una matriz en forma escalonada mediante operaciones elementales fila.

Diremos que una matriz tiene forma escalonada reducida si se cumplen:

En la forma escalonada reducida, un pivote es siempre 1 y suele llamarse "1 prinicipal".

Como una matriz \(A\) sólo es equivalente a una matriz con esta forma, suele llamarse "matriz FER de \(A\)" ó "\(FER(A)\)".

Obtención de la FER:

Podemos seguir los siguientes pasos para calcular la FER de una matriz:

1. Escribimos todas las matrices nulas en las últimas filas.
2. Si el primer elemento de la primera fila es 0, cambiamos la fila por otra cuyo primer elemento no sea 0. Si esto no es posible porque la primera columna es nula, consideramos que la primera columna no nula es la primera y volvemos a empezar desde 1, es decir, como si no tuviésemos la columna nula.
3. Dividimos la primera fila por el primer elemento no nulo de dicha fila para convertirlo en un 1.
4. Restamos a la fila i (todas excepto la primera) la primera fila multiplicada por el inverso del primer elemento de la fila i (si dicho elemento no es 0).
5. Ahora tenemos un uno principal en la primera fila (por encima y por debajo tiene 0's). Volvemos a aplicar el método al resto de la matriz como si la primera fila y primera columna no estuviesen.

Podéis encontrar ejemplos en la página eliminación de Gauss y de Gauss-Jordan

---