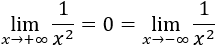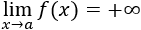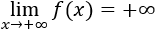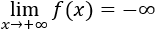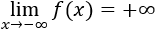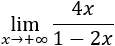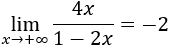Límite de una función (definiciones)

En esta página definimos el límite de una función y vemos algunos ejemplos, con las gráficas de las funciones.

Nota: el contenido de esta página es teórica (definiciones bastante técnicas). Para límites resueltos (práctica), vean las páginas:

• 50 límites resueltos
• Límites laterales
• Más límites resueltos
• Indeterminaciones

Contenido de esta página:

1. Límite finito de una función
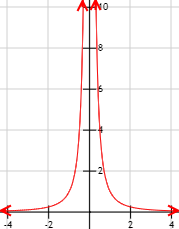
2. Límite infinito de una función
3. Ejemplos

Como las definiciones formales son distintas, tenemos que distinguir entre límites finitos e infinitos y límites cuando \(x\) tiende a un punto finito e infinito.

Las definiciones que proporcionamos no son únicas, así que podemos encontrar versiones parecidas. No obstante, el concepto es el mismo.

Vamos a distinguir dos casos: cuando \(x\) tiende a un punto finito y cuando \(x\) tiende a infinito.

Cuando \(x\) tiende a un punto finito \(a\):

Dada una función \(f:\mathbb{R}\rightarrow \mathbb{R}\), decimos que su límite es \(L\in\mathbb{R}\) cuando \(x\) se aproxima a \(a\in\mathbb{R}\) si \(\forall \varepsilon > 0\), \(\exists \delta >0\) tal que \(|f(x)-L|< \varepsilon \) siempre que \(|x-a|< \delta\). Lo denotamos por

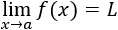
Interpretación:

Para todo \(\varepsilon > 0\), podemos encontrar un entorno del punto \(a\) tal que la diferencia de las imágenes de los puntos de dicho entorno es menor que \(\varepsilon\).

Dicho en otras palabras, la función toma valores tan próximos a \(L\) como queramos para algún entorno del punto \(x=a\).

Cuando \(x\) tiende a infinito:

Decimos que su límite es \(L\in\mathbb{R}\) cuando \(x\) tiende a \(+\infty\) si \(\forall \varepsilon > 0\), \(\exists K>0 \) tal que \(|f(x)-L|< \varepsilon \) siempre que \(x > K\). Lo denotamos por

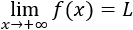
Análogamente, decimos que su límite es \(L\in\mathbb{R}\) cuando \(x\) tiende a \(-\infty\) si \(\forall \varepsilon > 0\), \(\exists K<0\) tal que \(|f(x)-L|< \varepsilon \) siempre que \(x < K\). Lo denotamos por

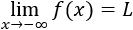
Nota: \(K\) es una constante dependiente de \(\varepsilon\) y realmente no es necesario exigir que sea positiva o negativa.

También, distinguimos cuando \(x\) tiende a un punto finito y cuando tiende a infinito.

Cuando \(x\) tiende a un punto finito \(a\):

Dada una función \(f:\mathbb{R}\rightarrow \mathbb{R}\), decimos que su límite es \(+\infty\) cuando \(x\) se aproxima a \(a\in\mathbb{R}\) si \(\forall K \in\mathbb{R}\), \(\exists \delta >0\) tal que \(f(x)> K \) siempre que \(|x-a|< \delta\). Lo denotamos por

Análogamente, su límite es \(-\infty\) cuando \(x\) se aproxima a \(a\in\mathbb{R}\) si \(\forall K\in\mathbb{R}\), \(\exists \delta >0\) tal que \(f(x)< K \) siempre que \(|x-a|< \delta\). Lo denotamos por

Interpretación:

La función toma valores tan grandes (primera definición) o tan pequeños (segunda definición) como queramos para algún entorno del punto \(x=a\).

Nota: la diferencia en las definiciones es que \(f(x)\) es mayor o menor que el número real \(K\) escogido.

Cuando \(x\) tiende a infinito:

Dada una función \(f:\mathbb{R}\rightarrow \mathbb{R}\), decimos que su límite es \(+\infty\) cuando \(x\) tiende a \(+\infty\) si \(\forall K \in\mathbb{R}\), \(\exists \delta >0\) tal que \(f(x)> K \) siempre que \(x > \delta\). Lo denotamos por

Análogamente, su límite es \(-\infty\) cuando \(x\) tiende a \(+\infty\) si \(\forall K \in\mathbb{R}\), \(\exists \delta >0\) tal que \(f(x)< K \) siempre que \(x > \delta\). Lo denotamos por

Cuando \(x\) tiende a menos infinito:

Dada una función \(f:\mathbb{R}\rightarrow \mathbb{R}\), decimos que su límite es \(+\infty\) cuando \(x\) tiende a \(-\infty\) si \(\forall K \in\mathbb{R}\), \(\exists \delta <0\) tal que \(f(x)> K \) siempre que \(x < \delta\). Lo denotamos por

Análogamente, su límite es \(-\infty\) cuando \(x\) tiende a \(-\infty\) si \(\forall K \in\mathbb{R}\), \(\exists \delta <0\) tal que \(f(x)< K \) siempre que \(x < \delta\). Lo denotamos por

Límite 1

Límite 2

Límite 3

Límite 4

Límite 5

---

---