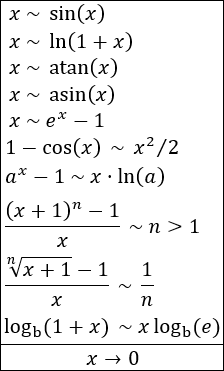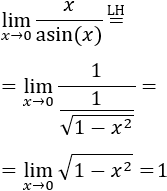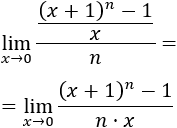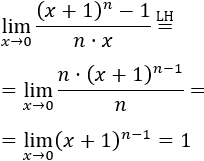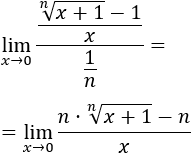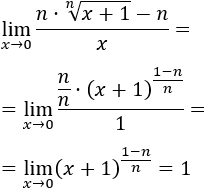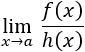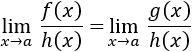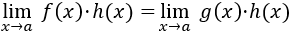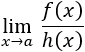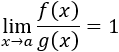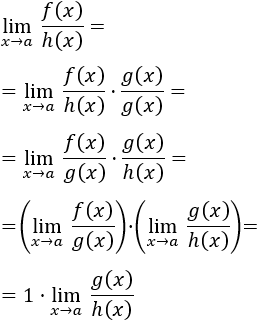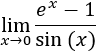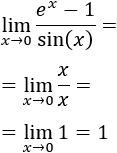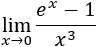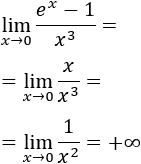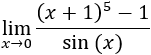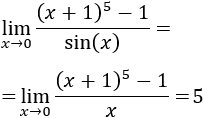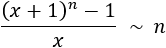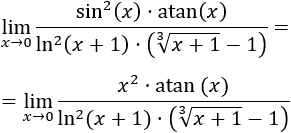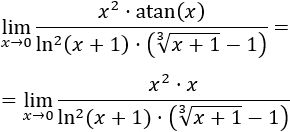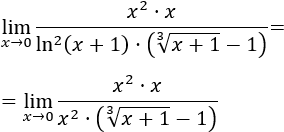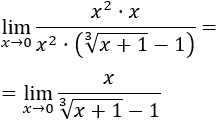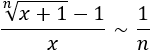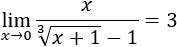Infinitésimos equivalentes

En esta página explicamos el concepto de infinitésimo e infinitésimo equivalente; demostramos algunos infinitésimos equivalentes y la propiedad que permite su aplicación; y calculamos algunos límites a modo de ejemplo.

Contenido de esta página:

1. Introducción
2. Algunos infinitésimos equivalentes (en \(x=0\))
3. Cálculo de límites
4. Ejemplos de aplicación

Los infinitésimos equivalentes son una importante herramienta en el cálculo infinitesimal ya que permiten calcular límites de productos o cocientes de funciones cambiando estas funciones por otras. Por ejemplo, el siguiente límite (Límite 5), sería bastante más complicado de calcular sin utilizar infinitésimos equivalentes:

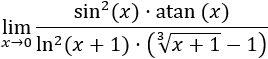
A continuación, definimos los conceptos necesarios.

Infinitésimo:

Sea \(f(x)\) una función \(f:\mathbb{R}\rightarrow\mathbb{R}\), se dice que es un infinitésimo en \(x=a\in\mathbb{R}\) si

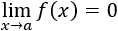
Infinitésimos equivalentes:

Dos infinitésimos \(f(x)\) y \(g(x)\) en \(x=a\) son equivalentes si se cumple

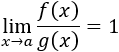
Lo denotamos por

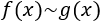
En esta página trabajaremos con infinitésimos equivalentes en \(x=0\).

Tabla con algunos infinitésimos equivalentes en \(x=0\):

Supongamos que existe el siguiente límite:

Si \(f(x)\) y \(g(x)\) son infinitésimos equivalentes en \(x=a\), entonces

También, podemos hacerlo en un producto:

Es decir, podemos sustituir un infinitésimo que multiplica o que divide por un infinitésimo equivalente.

Límite 1

Límite 2

Límite 3

Límite 4

Límite 5

---

---