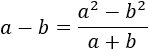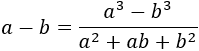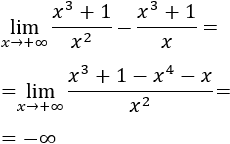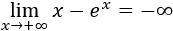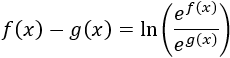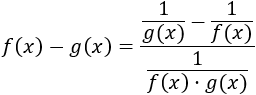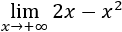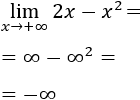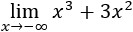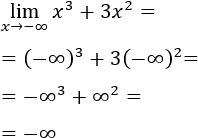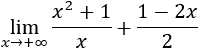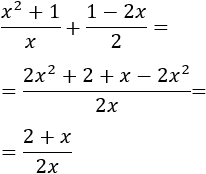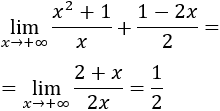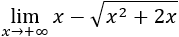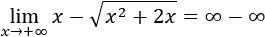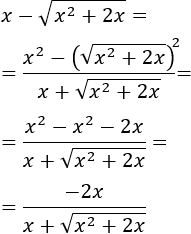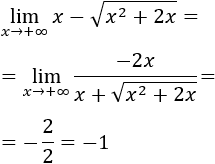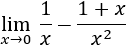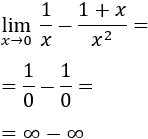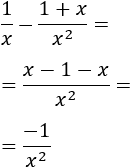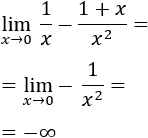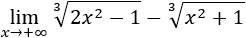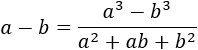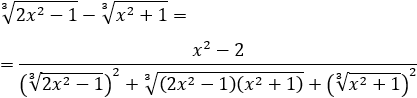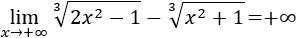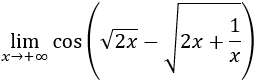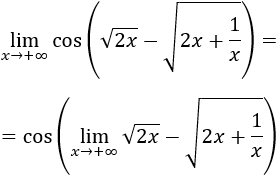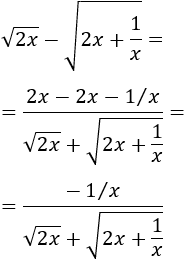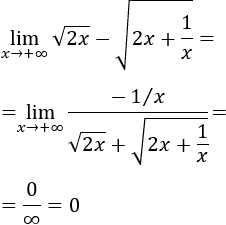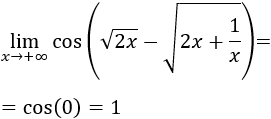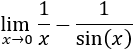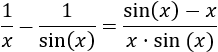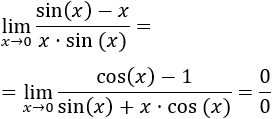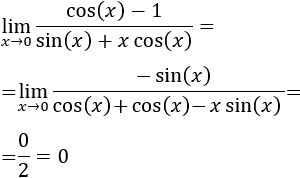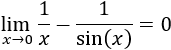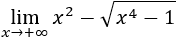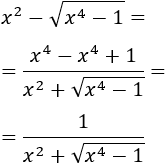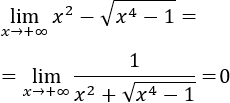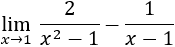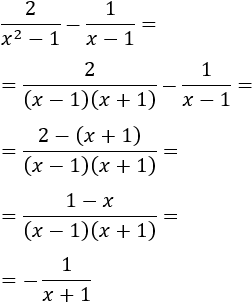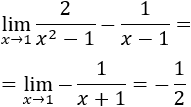Indeterminación infinito menos infinito, ∞-∞
En esta página hablamos sobre la indeterminación infinito menos infinito (\(\infty - \infty \)), viendo ejemplos y técnicas para evitar esta indeterminación.
Contenido de esta página:
- Introducción
- Algunos procedimientos
- Regla de L'Hôpital
- Límites resueltos
Páginas relacionadas
Otras páginas:
1. Introducción
Recordamos que una indeterminación o forma indeterminada es una expresión algebraica que aparece en el cálculo de límites y cuyo resultado no se puede conocer de antemano. Por ejemplo, la indeterminación \(\infty - \infty \) aparece en los siguientes límites:
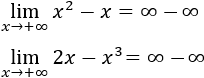
Las gráficas de estas funciones son
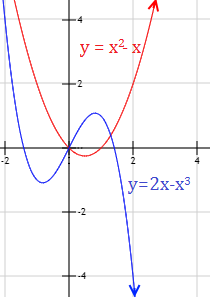
Por tanto, los límites anteriores son
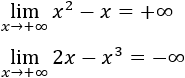
Estos resultados son intuitivos porque, tomando como ejemplo la función \(f(x) = x^2-x\) y dando valores a \(x\), tenemos:
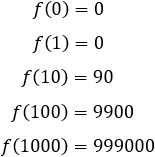
De donde podemos deducir
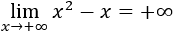
El monomio \(x^2\) crece más rápido que \(x\).
Por tanto, para obtener los resultados sin necesidad de las gráficas, tenemos que fijarnos en el orden de los infinitos. En el límite de un polinomio, la resta de infinitos es el infinito de mayor orden. El infinito que corresponde al monomio de grado mayor es el de mayor orden.
Por tanto,
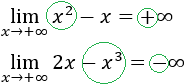
Por otro lado, cuando \(x\) tiende a infinito negativo, los límites coinciden:
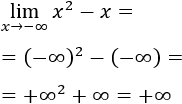
En el otro límite tenemos una resta de infinitos, así que nos quedamos con el de mayor grado:
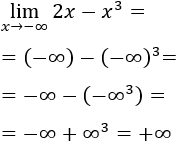
Veamos otro ejemplo:
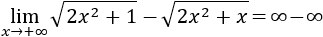
Podemos multiplicar y dividir por la suma de las raíces para eliminar la resta de raíces:
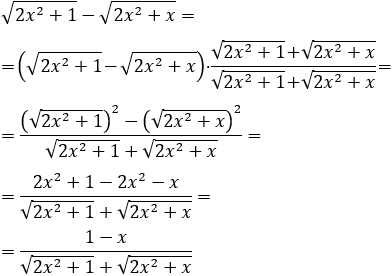
Por tanto,
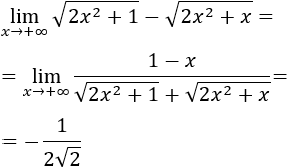
Nota: el resultado es el cociente de los coeficientes principales por tener el mismo grado en el numerador y denominador.
Resumiendo, hemos visto tres límites con la indeterminación infinito menos infinito y sus resultados son distintos. Esto justifica que \(\infty-\infty\) es una indeterminación.