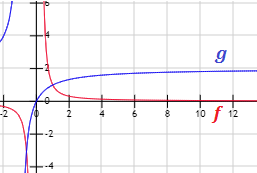
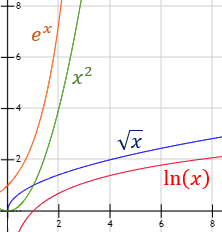
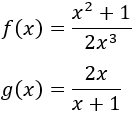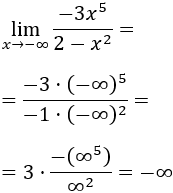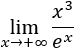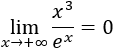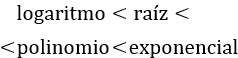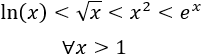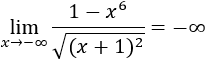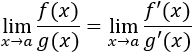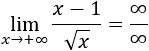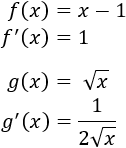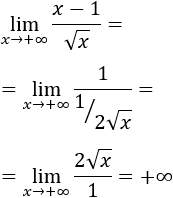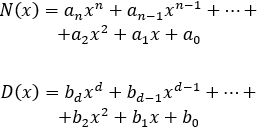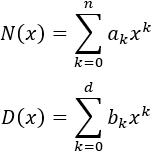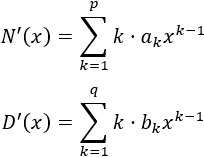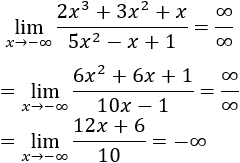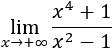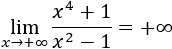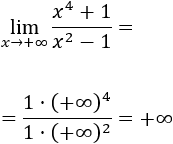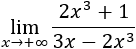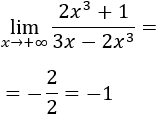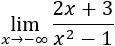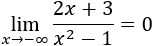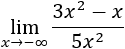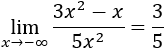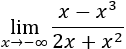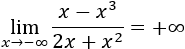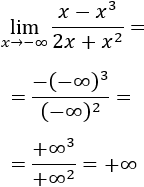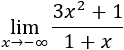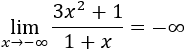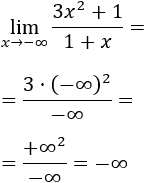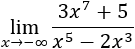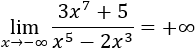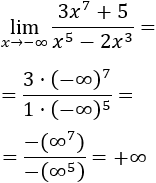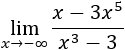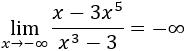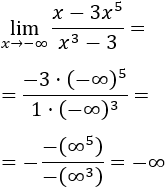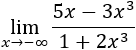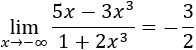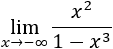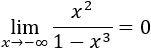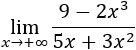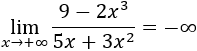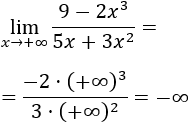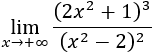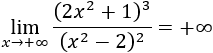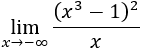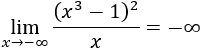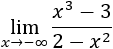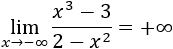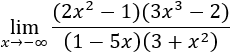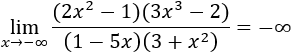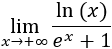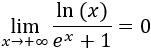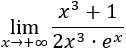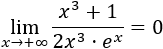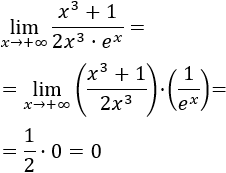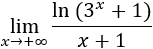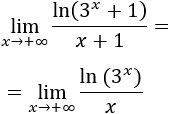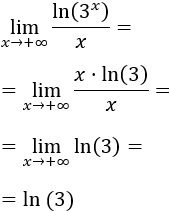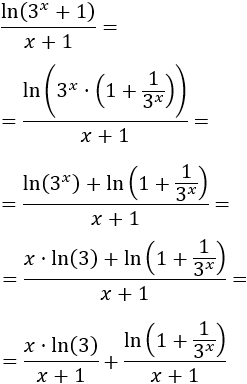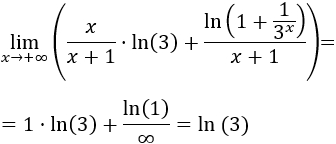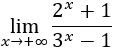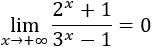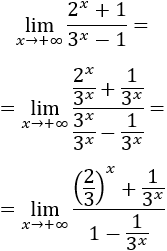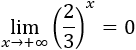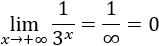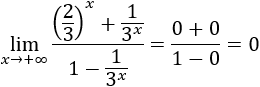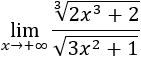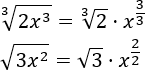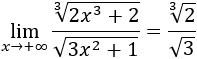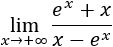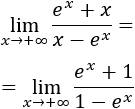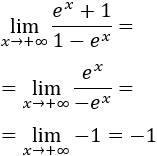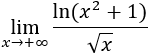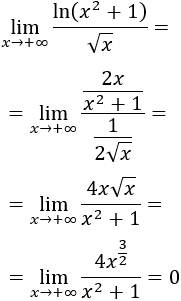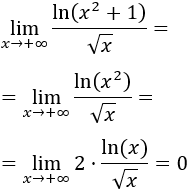Primero, resolvemos 15 límites de cocientes de polinomios. Después, 5 límites con otro tipo de cocientes. Finalmente, resolvemos 2 límites por la regla de L'Hôpital (más ejemplos en regla de L'Hôpital).
Cocientes de polinomios
Recordad que el razonamiento cambia un poco cuando \(x\to -\infty\), así que es es lo primero que hay que tener en cuenta. En la mayoría de los límites con \(x\to -\infty\), escribiremos, también, las potencias de infinitos para ver claramente el signo del resultado.
Límite 1
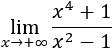
Solución
Tenemos la indeterminación infinito partido infinito, pero como el grado del numerador es mayor,
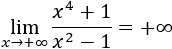
Si sirve de ayuda, podemos escribir las potencias de infinitos:
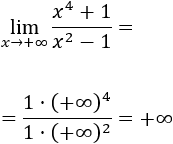
Límite 2
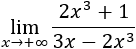
Solución
Tenemos la indeterminación infinito partido infinito, pero como los grados de los polinomios son iguales, el límite es el cociente de los coeficientes principales:
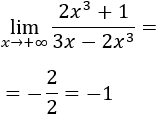
Límite 3
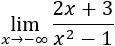
Solución
Tenemos la indeterminación infinito partido infinito, pero como el grado del denominador es mayor, el límite es \(0\):
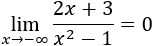
En este límite es irrelevante que \(x\) tienda a infinito positivo o negativo ya que el resultado es 0.
Límite 4
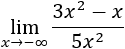
Solución
Tenemos la indeterminación infinito partido infinito, pero como los grados son iguales, el límite es el cociente de los coeficientes principales:
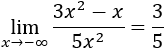
El resultado es el mismo si \(x\) tiende a infinito positivo.
Límite 5
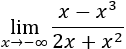
Solución
Tenemos la indeterminación infinito partido infinito.
Como el grado del numerador es mayor, el límite es infinito. Como el cociente de coeficientes es negativo y los exponentes son par e impar, el signo del infinito es positivo:
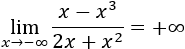
Si escribimos potencias de infinitos, tenemos
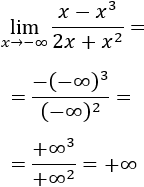
El cubo es negativo y el cuadrado es positivo, pero como hay un signo negativo delante del cubo, su resultado es positivo.
Límite 6
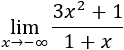
Solución
Tenemos la indeterminación infinito partido infinito.
El grado del numerador es mayor, el cociente de los coeficientes es positivo y los exponentes son par e impar. Por tanto,
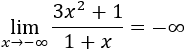
Si escribimos potencias de infinitos,
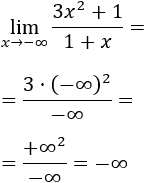
Límite 7
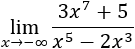
Solución
El grado del numerador es mayor, los exponentes son impares y el cociente de los coeficientes es positivo. Por tanto, el resultado es infinito positivo:
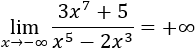
Si escribimos las potencias de infinitos,
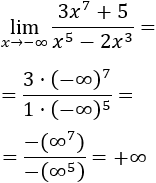
Observad que, al ser los dos exponentes impares, las potencias son negativas. Estos signos se cancelan al ser iguales.
Límite 8
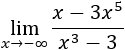
Solución
El grado del numerador es mayor, el cociente de los coeficientes principales es negativo y los grados son impares. Por tanto,
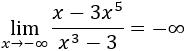
Si escribimos potencias de infinitos,
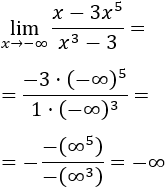
Límite 9
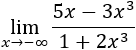
Solución
Como los grados son iguales, el límite es
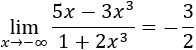
Límite 10
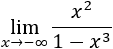
Solución
Como el polinomio del denominador es de grado mayor,
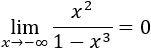
Límite 11
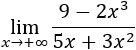
Solución
Como grado del numerador es mayor y el cociente de los coeficientes principales es negativo,
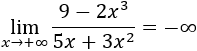
Si escribimos potencias de infinitos,
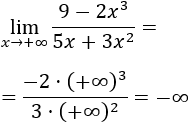
Límite 12
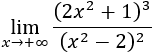
Solución
Si desarrollamos las potencias, tendremos un polinomio de grado 6 en el numerador y uno de grado 4 en el denominador. Por tanto, el límite es infinito.
El monomio de grado mayor del numerador sería \(8x^6\) y el del denominador sería \(x^4\). Como los coeficientes son positivos, el infinito es positivo:
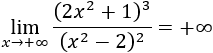
Límite 13
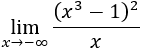
Solución
El grado del numerador es \(6\) y el del denominador es \(1\). El cociente de sus coeficientes es positivo y los exponentes son par e impar. Por tanto,
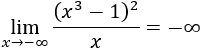
Límite 14
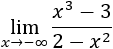
Solución
Como el grado del numerador es mayor, los grados son impar y par y el cociente de los coeficientes es negativo,
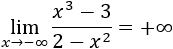
Límite 15
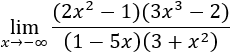
Solución
Si multiplicamos los polinomios, el monomio de grado mayor del numerador es \(6x^5\) y el del denominador es \(-5x^3\). Por tanto, el límite es
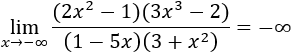
Límites de otros tipos de cocientes
En los siguientes 5 límites vamos a comparar el crecimiento de las funciones.
Límite 16
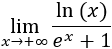
Solución
Tenemos la indeterminación infinito partido infinito, pero la función del denominador crece más rápidamente por ser una exponencial. Por tanto,
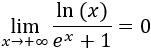
Límite 17
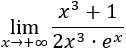
Solución
Los grados del numerador y denominador son iguales, pero hay una exponencial en el denominador. Por tanto,
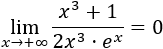
También, podemos escribir la función como un producto:
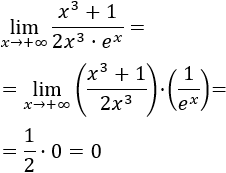
El límite del factor de la izquierda tiende a 1/2 porque es un cociente de polinomios de igual grado. El límite del otro factor es 0 porque le denominador tiende a infinito.
Límite 18
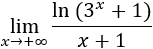
Solución
Como el logaritmo de infinito es infinito, tenemos la indeterminación infinito partido infinito.
En un principio, el polinomio del denominador tiene más peso que un logaritmo, pero el logaritmo del numerador tiene una exponencial. Esto complica la comparación.
Como estamos trabajando con límites, cuando \(x\) es muy grande, la diferencia entre \(3^x\) y \(3^x+1\) es insignificante. Lo mismo ocurre con \(x\) y \(x+1\). Por esta razón, podemos omitir estos dos sumandos \(+1\):
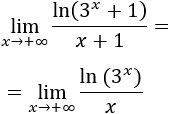
De este modo, podemos aplicar las propiedades del logaritmo:
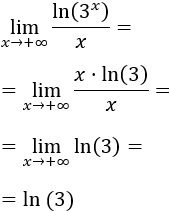
Si no vemos claro el razonamiento anterior, podemos proceder de otro modo más técnico, operando:
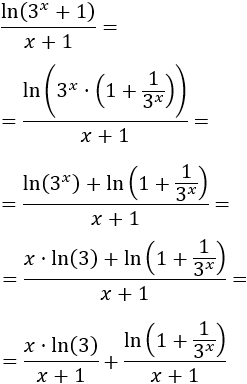
Tomando límites,
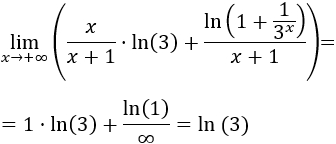
El límite del sumando de la derecha es 0 porque tenemos 0 entre infinito.
Límite 19
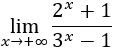
Solución
Como las exponenciales tienden a infinito, tenemos la indeterminación infinito partido infinito, pero como la base de la exponencial del denominador es mayor, prima. Por tanto, el límite es \(0\):
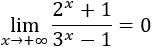
Otro modo de resolver el límite es dividir entre la exponencial de mayor base (\(3^x\)):
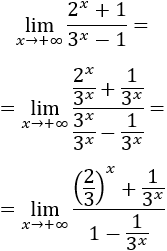
Como \(2/3\) es menor que \(1\), sus potencias tienden a \(0\):
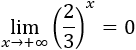
El límite de las otras fracciones es
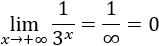
Por tanto,
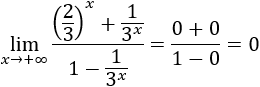
Límite 20
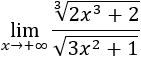
Solución
Tenemos un cociente de infinitos. Podemos razonar del mismo modo que hacemos con los cocientes de polinomios.
Si pensamos en las raíces como potencias, los monomios principales de los polinomios son
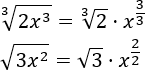
Los dos grados son iguales, por tanto,
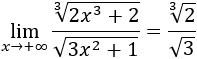
Límites por L'Hôpital
Límite 21
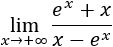
Solución
Se ve claramente que el límite es -1, pero como tenemos la indeterminación infinito entre infinito, podemos aplicar la regla de L'Hôpital:
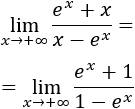
Como seguimos teniendo la misma indeterminación, aplicamos la regla de nuevo:
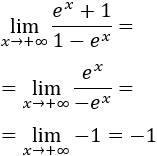
Límite 22
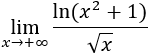
Solución
Tenemos la indeterminación infinito dividido infinito, así que podemos aplicar la regla de L'Hôpital:
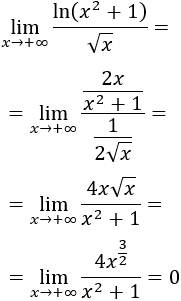
El límite es \(0\) porque el grado del polinomio del denominador es mayor.
También, podemos calcular el límite rápidamente sin aplicar la regla. Cuando \(x\) es grande, podemos cambiar el logaritmo de \(x^2+1\) por el de \(x^2\):
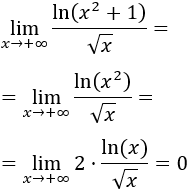
El límite es \(0\) porque la raíz crece más rápido que el logaritmo.
Enlace: 50 límites resueltos


Indeterminación infinito partido infinito (∞/∞) - © matesfacil.com

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.