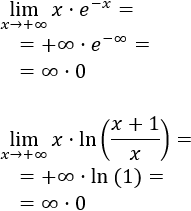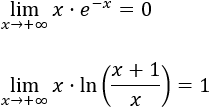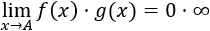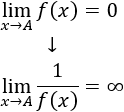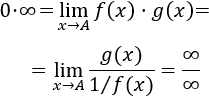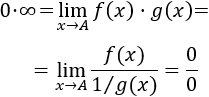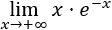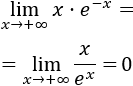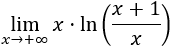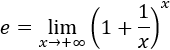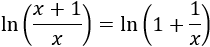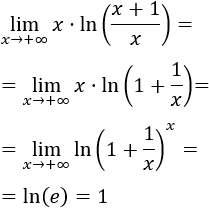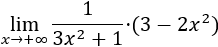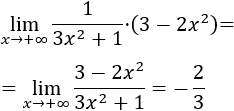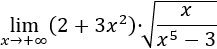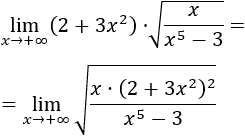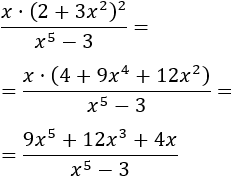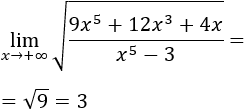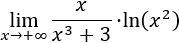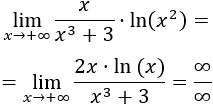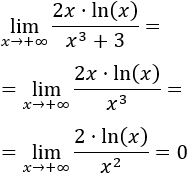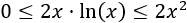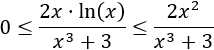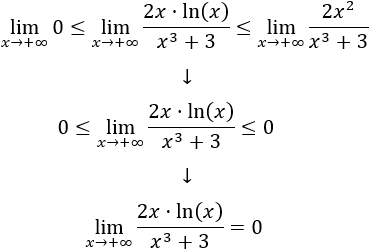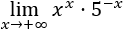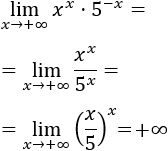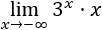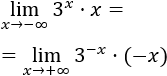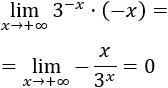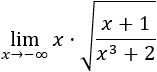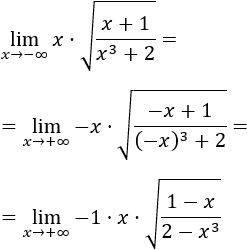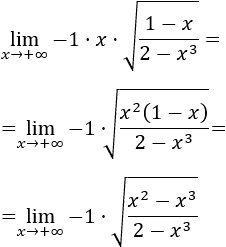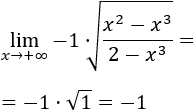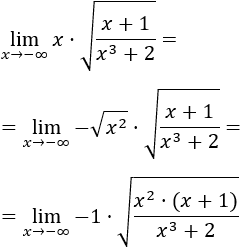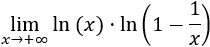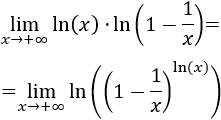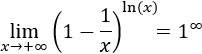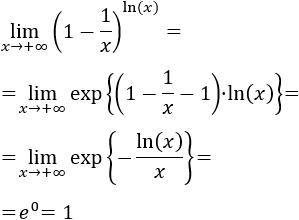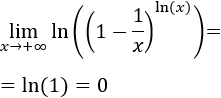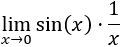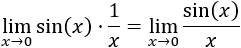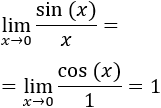Nota: sólo aplicamos la regla de L'Hôpital en el último límite. Más ejemplos en regla de L'Hôpital.
Límite 1
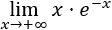
Solución
El factor \(x\) tiende infinito. El factor \(e^{-x}\) tiende a 0 porque la base es mayor que 1 y el exponente tiende a \(-\infty\).
Es fácil escribir el producto como un cociente al cambiar el signo del exponente, apareciendo así la indeterminación infinito partido infinito:
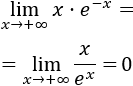
El límite es 0 porque el crecimiento de la exponencial es mayor que el de \(x\).
Límite 2
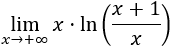
Solución
Recordad que el número \(e\) es el límite de una función:
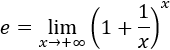
Observad que el argumento del logaritmo es la base de la exponencial del límite anterior:
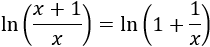
Por tanto, aplicando las propiedades de los logaritmos,
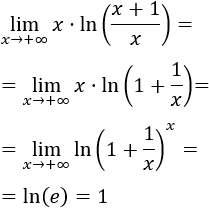
Límite 3
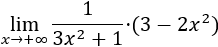
Solución
Sólo tenemos que escribir el factor de la derecha en el numerador para tener la indeterminación infinito partido infinito:
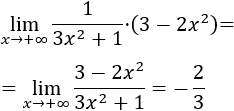
El límite es el cociente de los coeficientes principales de los polinomios porque tienen el mismo grado.
Límite 4
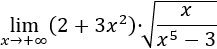
Solución
El polinomio de la izquierda tiende a infinito. El radicando tiende a 0 porque el grado del polinomio del denominador es mayor que el del numerador, así que su raíz tiende también a 0.
Podemos introducir el factor de la izquierda (es positivo) en la raíz escribiendo su cuadrado:
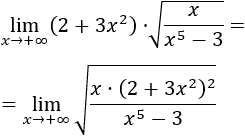
Desarrollamos el cuadrado:
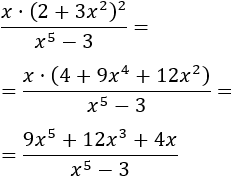
El límite de este cociente de polinomios es 9 porque los grados de los polinomios son iguales. Por tanto,
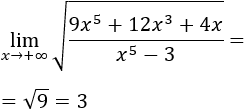
Límite 5
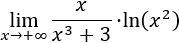
Solución
La fracción tiende a 0 porque el grado del polinomio del denominador es mayor que el del numerador. El logaritmo tiende a infinito.
Operando un poco, tenemos la indeterminación infinito partido infinito:
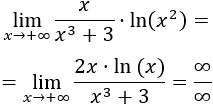
En el numerador tenemos el monomio \(x^3\), mientras que en el numerador tenemos \(2x·ln(x)\).
Como \(x\) tiende a \(\infty\), el sumando \(+3\) del denominador es insignificante, por lo que podemos omitirlo*:
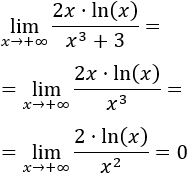
El límite es 0 porque el monomio \(x^2\) crece más rápido que el logaritmo.
Nota*: podemos ser más técnicos, aplicando el criterio del emparedado:
Como \(x\) tiende a \(+\infty\), podemos suponer que \(x> 1\). En este caso, como \(ln(x)\) es menor que \(x\),
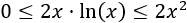
Dividiendo entre \(x^3+3> 0\),
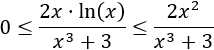
El cociente de polinomios de la derecha tiende a 0 porque el grado del polinomio del denominador es mayor. Por tanto, aplicando límites (criterio del emparedado), tenemos,
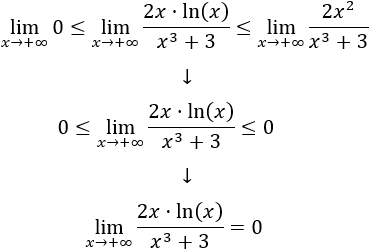
Límite 6
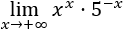
Solución
Como infinito elevado a infinito es infinito, tenemos la indeterminación \(\infty ·0\).
Podemos escribir la exponencial en el denominador:
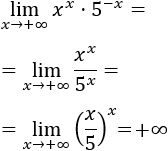
El límite es infinito porque tenemos infinito elevado a infinito.
Límite 7
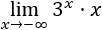
Solución
Observad que \(x\) tiende a infinito negativo.
Si cambiamos el signo de las \(x\), podemos escribir \(x\to+\infty\) en el límite:
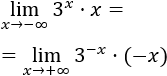
Así es más fácil calcular el límite:
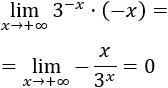
El límite es 0 porque la exponencial crece más rápido.
Límite 8
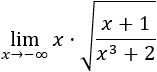
Solución
Observad que \(x\) tiende a infinito negativo.
Cambiamos el signo de las \(x\) para escribir el límite con \(x\to +\infty\):
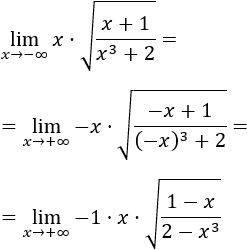
Introducimos la \(x\) (es positiva) en la raíz:
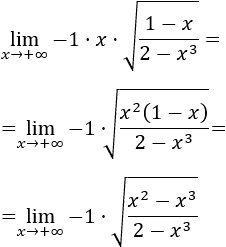
El límite del cociente de polinomios es \(1\) (el cociente de sus coeficientes principales) porque tienen el mismo grado. Por tanto,
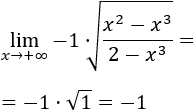
Para calcular el límite sin cambiar \(x\to -\infty\), tenemos que ser más cuidadosos porque \(x\) toma valores negativos cuando \(x\) tiende a infinito negativo.
-
Si \(x\) es positiva, \(x=\sqrt{x^2}\)
-
Si \(x\) es negativa, \(x = -\sqrt{x^2}\)
En el límite, \(x\) toma valores negativos, así que
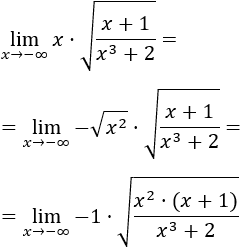
Límite 9
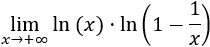
Solución
Tenemos la indeterminación infinito por cero.
Aplicamos las propiedades de los logaritmos:
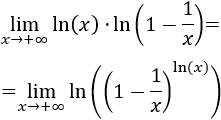
Aparece la indeterminación 1 elevado a infinito en el argumento:
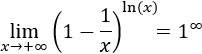
Aplicamos la fórmula que tenemos para evitar esta indeterminación:
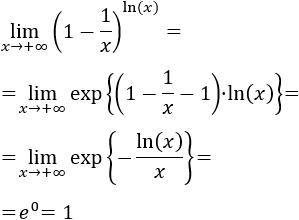
Por tanto, el argumento tiende a 1 y, como consecuencia, el límite es 0:
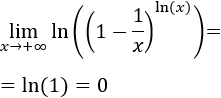
Límite 10
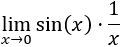
Solución
Es fácil ver que tenemos la indeterminación 0 partido 0:
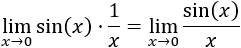
Aplicamos L'Hôpital (derivamos numerador y denominador):
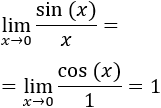


Indeterminación cero por infinito (0·∞), con límites resueltos - © matesfacil.com

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.