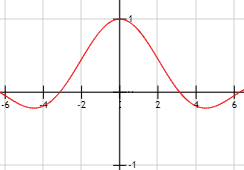
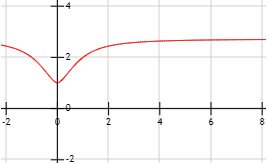
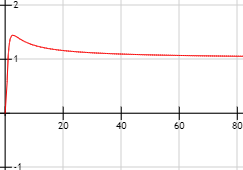
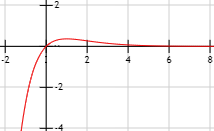
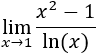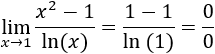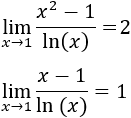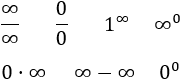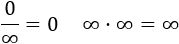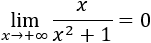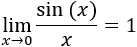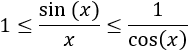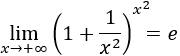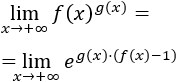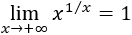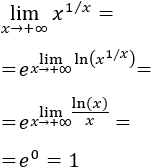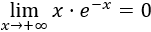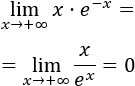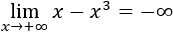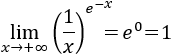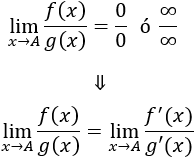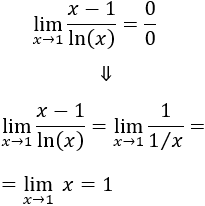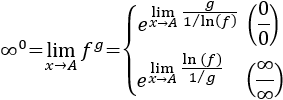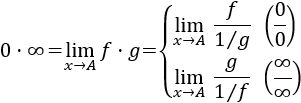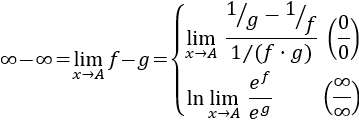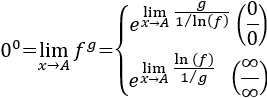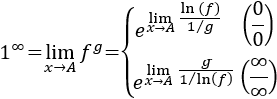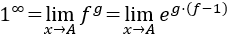Indeterminación o forma indeterminada
En esta página explicamos qué es una indeterminación matemática, calculamos algunos límites que presentan indeterminaciones y proporcionamos las transformaciones que permiten aplicar la regla de L'Hôpital.
Contenido de esta página:
- Introducción
- Indeterminación
- Ejemplos
- Transformaciones para aplicar L'Hôpital
Páginas relacionadas
Otras páginas:
1. Introducción
Recordamos el concepto intuitivo de límite:
Sea \(f(x)\) una función y sea \(a\) un punto, el límite de \(f(x)\) cuando \(x\) tiende a \(a\) es el valor al que se aproxima \(f(x)\) cuando \(x\) se aproxima a \(a\).
Por ejemplo, el límite de \(f(x) = x^2\) cuando \(x\) tiende a 2 es 4:
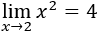
Podemos dar valores a \(x\) cercanos a 2 por su izquierda:
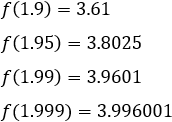
Y por su derecha,
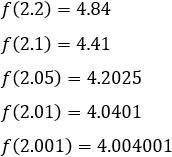
Observamos que, cuanto más se aproxima \(x\) a 2, más se aproxima \(f(x)\) a 4 (por ambos lados). Por tanto, el límite de \(f(x)\) en \(x=2\) es 4.
En realidad, también podemos calcular el límite anterior sustituyendo \(x=2\) en el límite:
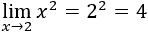
Nota: no siempre el límite de \(f(x)\) en \(x=a\) coincide con \(f(a)\).