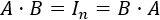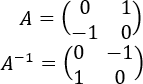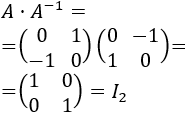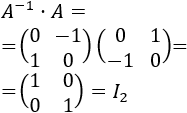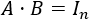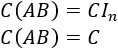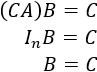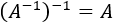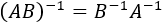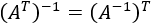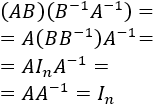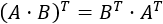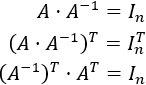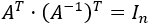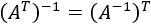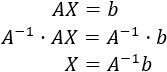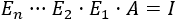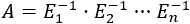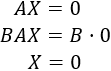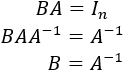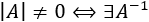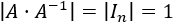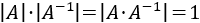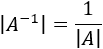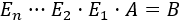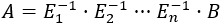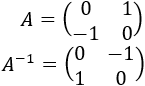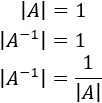Sean \(A\) y \(B\) dos matrices regulares de dimensión \(n\), entonces:
-
La matriz inversa de \(A\), \(A^{-1}\), es regular y su inversa es \(A\):
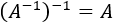
-
Inversa del producto de matrices:
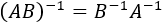
-
Inversa de la matriz traspuesta:
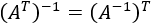
Ver demostración
Inversa de la inversa:
La demostración es directa.
Inversa del producto:
Como \(A\) y \(B\) tienen inversas, sólo tenemos que multiplicar por ellas y aplicar la propiedad asociativa del producto matricial:
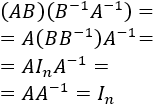
Si calculamos el producto \((B^{-1}A^{-1})(AB)\) también obtenemos la matriz identidad. Por tanto, la inversa de \((AB)\) es \((AB)^{-1} = B^{-1}A^{-1}\).
Inversa de la traspuesta:
Recordad que la traspuesta de la identidad es la identidad y la traspuesta del producto de matrices es
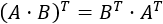
Como \(A\) por \(A^{-1}\) es la identidad,
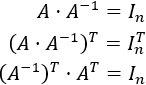
De forma análoga,
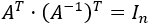
Las dos últimas igualdades significan que la inversa de \(A^T\) es \((A^{-1})^T\):
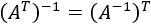
El producto de matrices regulares es una matriz regular.
La demostración es consecuencia directa del apartado 2: el producto de dos matrices regulares es una matriz regular porque existe la inversa del producto.
Destacamos las dos siguientes caracterizaciones de la matriz inversa, aunque, sin duda, la segunda de ellas (Teorema 2) es la más importante. También veremos un corolario interesante.
Teorema 1
Sea \(A\) una matriz de dimensión \(n\). Las siguientes condiciones son equivalentes (ocurren todas las condiciones simultáneamente o ninguna de ellas):
-
La matriz \(A\) es regular (invertible).
-
Todo sistema de ecuaciones lineales (SEL) con matriz de coeficientes \(A\) (es decir, \(AX=b\)) es compatible determinado.
-
El SEL homogéneo \(AX=0\) es compatible determinado.
-
La forma escalonada de \(A\) es la matriz identidad \(I_n\).
-
La matriz \(A\) es producto de matrices elementales.
Ver demostración
(\(1\rightarrow 2\))
Si la matriz \(A\) es regular, existe su inversa \(A^{-1}\). Multiplicando el sistema por la inversa, tenemos
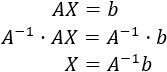
Por tanto, la única solución del sistema es \(X = A^{-1}b\).
(\(2\rightarrow 3\))
Como la solución del SEL \(AX=b\) es \(A^{-1}·b\), si \(b\) es la matriz columna de 0's, tenemos que el SEL homogéneo \(AX = 0\) es compatible determinado.
(\(3\rightarrow 4\))
Como el SEL \(AX = 0\), la forma escalonada reducida de \(A\) es la matriz identidad.
(\(4\rightarrow 5\))
Si la forma escalonada reducida de \(A\) es la identidad, entonces existen matrices elementales \(E_1\), \(E_2\),…,\(E_n\) tales que
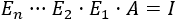
Como las matrices elementales son regulares, multiplicando en la igualdad anterior por sus inversas, tenemos que la matriz \(A\) es un producto de matrices regulares:
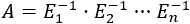
(\(5\rightarrow 1\))
Ya vimos en las propiedades de la inversa que el producto de matrices regulares es una matriz regular.
Dada una matriz \(A\), el producto por ambos lados por su inversa debe ser la identidad. El siguiente corolario afirma que es suficiente con que se cumpla para un lado, es decir,
Corolario
Sean \(A\) y \(B\) dos matrices cuadradas. Si \(BA=I_n\) ó \(AB=I_n\), entonces \(A\) es invertible y su inversa es \(A^{-1}=B\).
Además, se tiene que \(B\) es invertible y su inversa es \(B^{-1}=A\).
Ver demostración
Supongamos \(BA=I_n\).
El sistema \(AX=0\) es compatible determinado porque, si multiplicamos por \(B\), tenemos
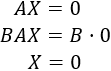
Por el teorema anterior, como \(AX=0\) es compatible determinado, la matriz \(A\) es regular y tiene inversa. Multiplicando por la inversa de \(A\) en la igualdad \(BA=I_n\),
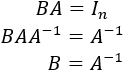
Se demuestra de forma análoga si suponemos \(AB=I_n\).
Teorema 2
Una matriz \(A\) es regular (tiene inversa) si, y solamente si, su determinante es distinto de 0:
Es decir,
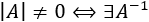
Ver demostración
\((\leftarrow )\)
Supongamos que la matriz \(A\) tiene inversa. Entonces,
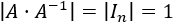
Como el determinante de un producto de matrices es el producto de los determinantes de las matrices,
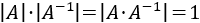
Por tanto, el determinante de \(A\) y el de \(A^{-1}\) son distintos de 0 y, además,
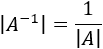
\((\rightarrow )\)
Demostraremos el contrarecíproco, es decir, que si \(A\) no tiene inversa, entonces su determinante es 0.
Si la matriz \(A\) no es invertible, entonces su forma escalonada reducida, \(B\), no es la identidad (por el teorema 1), así que tiene al menos una fila de 0's.
Por otro lado, sabemos que existen matrices elementales \(E_1\), \(E_2\),…\(E_n\) tales que
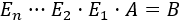
Como las matrices elementales son regulares,
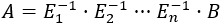
Por la forma de \(B\), su determinante es 0 y, como el determinante del producto es el producto de los determinantes, el determinante de \(A\) es 0.
Ver ejemplo
Sean las matrices
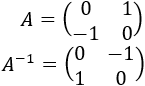
Sus determinantes son
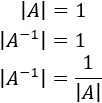


Matriz inversa (teoría) -
© matesfacil.com

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.