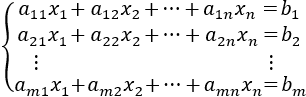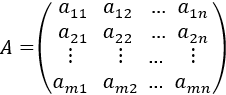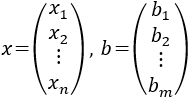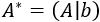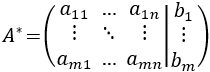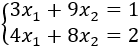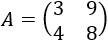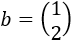Matrices y sistemas de ecuaciones
En esta página vamos a ver por qué el álgebra matricial es una gran herramienta para estudiar y resolver sistemas de ecuaciones lineales. El texto es más bien teórico, pero se incluyen enlaces a problemas resueltos.
Contenido de esta página:
- Introducción
- Definición de SEL y su representación matricial
- Clasificación de los SEL según su forma
- Solución de un SEL y número de soluciones
- Métodos para resolver un SEL
- Teorema de Rouché-Frobenius
Páginas relacionadas
Páginas amigas:
1. Introducción
Una de las aplicaciones más importantes del álgebra matricial es la resolución de sistemas de ecuaciones lineales (SEL). En esta página vamos ver cómo representar un SEL en forma matricial y algunos resultados teóricos del álgebra matricial que permiten clasificarlo y resolverlo.
Sin duda, el resultado más relevante es el teorema de Rouché-Frobenius, que nos permite clasificar el SEL a partir del rango de la matriz ampliada del SEL.
Asumimos que ya conocemos el concepto de matriz y sus operaciones básicas (suma, resta, producto, transpuesta, determinante, matriz inversa, rango, etc.).
Notación: llamaremos \(x_i\) a las incógnitas de los sistemas para poder hablar de forma genérica de un sistema con \(n\) incógnitas.