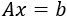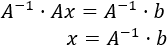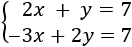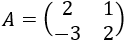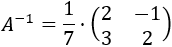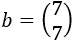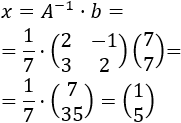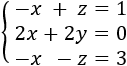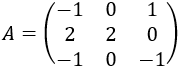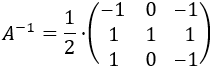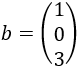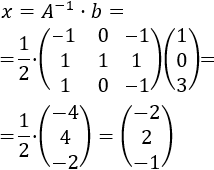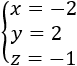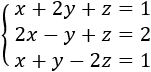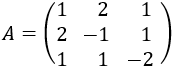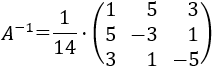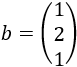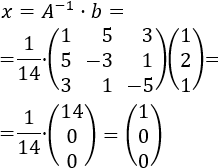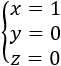Supongamos que tenemos un sistema de \(n\) ecuaciones lineales con \(n\) incógnitas. Podemos representar el sistema de forma matricial como
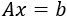
donde
-
La matriz \(A\) es de dimensión \(nxn\) y contiene en cada fila los coeficientes de las incógnitas de cada ecuación.
-
La matriz \(x\) es de dimensión \(nx1\) (una columna) y contiene las \(n\) incógnitas del sistema.
-
La matriz \(b\) es de dimensión \(nx1\) y contiene los términos independientes de las ecuaciones.
Si el sistema tiene una única solución (es compatible determinado), entonces la matriz \(A\) es regular (determinante distinto de 0) y, por tanto, existe su matriz inversa \(A^{-1}\).
Entonces, podemos multiplicar toda la ecuación por la inversa de \(A^{-1}\):
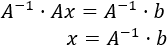
Es decir, si la matriz \(A\) es regular, entonces la matriz columna resultante del producto matricial \(A^{-1}·b\) contiene la solución del sistema \(Ax=b\).
En esta página vamos a ver 3 ejemplos de este método.
Sistema 1
Sistema de 2 ecuaciones con 2 incógnitas (2x2)
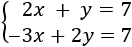
Ver solución
La matriz de coeficientes del sistema es
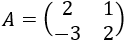
Es una matriz regular porque su determinante es 7. Su matriz inversa es
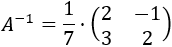
La matriz de términos independientes del sistema es
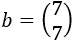
Calculamos la solución del sistema multiplicando las matrices \(A^{-1}\) y \(b\):
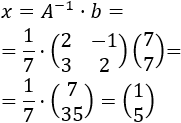
Por tanto, la solución del sistema es

Sistema 2
Sistema de 3 ecuaciones con 3 incógnitas (3x3)
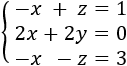
Ver solución
La matriz de coeficientes del sistema es
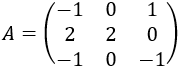
Es una matriz regular porque su determinante es 4. Su matriz inversa es
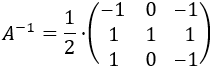
La matriz de términos independientes del sistema es
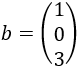
Calculamos la solución del sistema multiplicando las matrices \(A^{-1}\) y \(b\):
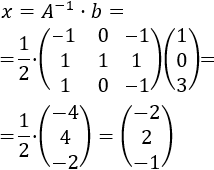
Por tanto, la solución del sistema es
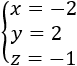
Sistema 3
Sistema de 3 ecuaciones con 3 incógnitas (3x3)
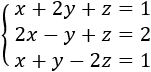
Ver solución
La matriz de coeficientes del sistema es
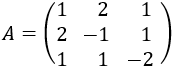
Es una matriz regular porque su determinante es 14. Su matriz inversa es
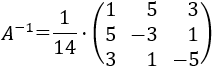
La matriz de términos independientes del sistema es
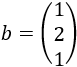
Calculamos la solución del sistema multiplicando las matrices \(A^{-1}\) y \(b\):
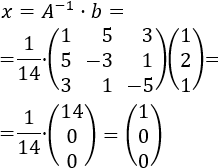
Por tanto, la solución del sistema es
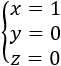


Método de la inversa para resolver sistemas de ecuaciones -
© matesfacil.com

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.